Hallo,
Willkommen in der Mathelounge!
Die Volumina oben \(V_o\) zu unten \(V_u\) verhalten sich wie \(3\div 5\). Und wenn Dir die Volumenformel, die Fläche des Trapez, Sätze über änliche Dreiecke und Seitenhalbierende im Dreieck vertraut sind, sollte das lösbar sein.
Ich unterstelle, dass die Grundfläche der Pyramide mindestens rechteckig (quadratisch ist Ok) ist und die Spitze \(S\) sich senkrecht oberhalb der Mitte \(M\) der Grundfläche befindet.
Das erste Ziel ist es, die Höhe der Spitze \(S\) über der Schnittfläche zu bereche. Mit dem Ziel, das Volumen \(V_o\) des oberen Pyramidenteils zu berechnen. Dazu habe ich hier eine Schnitt durch die Pyramide gezeichnet, der senkrecht auf der Grundfläche steht.
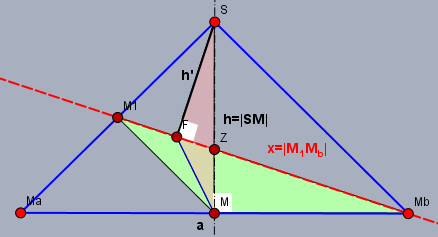
Die Schnittlinie ist die rot gestrichelte Gerade durch \(M_1M_b\). Die gesuchte Höhe \(h'= |FS|\) ist schwarz markiert. Die Höhe der Pyramide sei \(h\) und die Länge der Kante, die parallel zur Zeichenebene verläuft, sei \(a\).
Zunächst soll gezeigt werden, dass die farbig markierten Dreiecke \(\triangle MM_bM_1\) (grün) und \(\triangle MSF\) (rosa) änlich sind. Die beiden rechtwinkligen Dreiecke \(\triangle FZS\) und \(\triangle MM_bZ\) sind offensichtlich ähnlich, da sie bei \(Z\) einen gemeinsamen Winkel haben.
Der Punkt \(Z\) ist der Schnittpunkt der Seitenhalbierenden im Dreieck \(\triangle M_aM_bS\) und teilt folglich die Strecken \(|M_bM_1|\) und \(|SM|=h\) im Verhältnis \(2\div 1\). Daraus folgt, dass es sich bei den Seiten \(|M_bM_1|\) und \(h\) um die um den selben(!) Faktor \(3/2\) verlängerten Hypotenusen der beiden oben erwähnten rechtwinkligen Dreiecke handelt.
Und daraus folgt, dass \(\triangle MM_bM_1\) und \(\triangle MSF\) änlich sind!
Die Strecke \(|M_bM_1|\) nenne ich \(x\) (rot), dann gilt$$\frac{h'}{h} = \frac{a/2}{x} \implies h' = \frac{ah}{2x}$$Die Schnittfläche ist ein Trapez und seine Fläche ist$$F_T= \frac 12 \left(\frac b2 + b\right)x = \frac34 bx$$wenn \(b\) die Kantenlänge der Grundfläche der Pyramide ist, die senkrecht zur Zeichenebene verläuft. Beachte dass \(x\) auch die Höhe des Trapez ist!
Und somit ist das Volumen \(V_o\) des oberen Teils$$V_o = \frac 13 h' F_T = \frac 13 \cdot \frac{ah}{2x} \cdot \frac34 bx=\frac 18 hab$$Jetzt ziehe diesen Wert vom Gesamtvoluimen \(hab/3\) ab und setze beide in's Verhältnis.
Gruß Werner