Hallo,
zeichne zuerst ein Rechteck mit den Seitenlängen 4 und 5. Das kann 4cm und 5cm oder eine andere Einheit, Hauptsache das Verhältnis stimmt. Zeichne die Diagonalen ein und wähle den Schnittpunkt \(M\) der Diagonalen als Mittelpunkt des Kreises und zeichen diesen mit \(r = 5\,\text{cm}\).
Verlängere die Diagonalen, so dass sie den Kreis schneiden. Die vier Schnittpunkte der beiden Diagonalen mit dem Kreis sind die Eckpunkte des gesuchten Rechtecks.
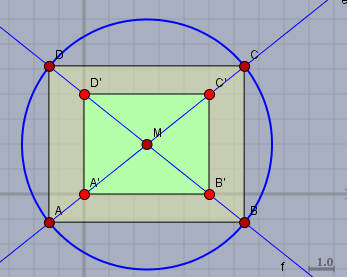
falls der Kreis selbst bereits vorgegen ist, kannst Du obige Konstruktion als Hilfskonstruktion nutzen und die Seitenlängen dann auf den gegebenen Kreis übertragen oder eine alternative Konstruktion mit Hilfe des Kreises des Apollonios nutzen:
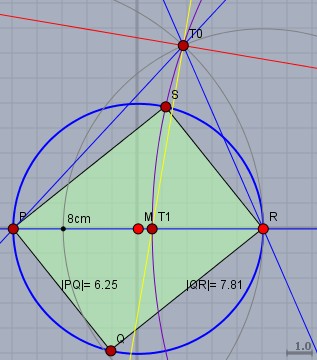
Zeichne eine Gerade \(e\) durch den Mittelpunkt \(M\) des Kreises, die den Kreis in \(P\) und \(R\) schneidet. Zeichne um \(R\) einen Kreis mit \(8\,\text{cm}\) und um \(P\) einen Kreis mit \(10\,\text{cm}\) Radius. Die Kreise schneiden sich oberhalb von \(e\) in \(T_0\). Konstruiere die Winkelhalbierende (gelb) der Geraden durch \(PT_0\) und \(RT_0\) sowie deren Orthogonale (rot) durch \(T_0\). Die Winkelhalbierende und ihre Orthogonale schneiden \(e\) in \(T_1\) und \(T_2\).
Nun zeichne einen Kreis (lila) mit Mittelpunkt \(M_T\) (dem Mittelpunkt von \(|T_1T_2|\)) durch \(T_1\), der den Ausgangskreis oberhalb von \(e\) in \(S\) schneidet. Spiegele \(S\) an \(M\) zu \(Q\). \(PQRS\) ist das gesuchte Rechteck.
Gruß Werner