Welcher Punkt P ist von S1, S2 und S3 gleich weit entfernt?

Question

S1(-2/0)

S2(0/-4)

S3(4/0)

Ich soll nun den Punkt P ermitteln der gleich weit entfernt von S1-3 liegt.

Meine Mathe-Lehrerin sagte, ich könnte einfach Gleichungen aufstellen und hätte dann 2 Unbekannte.

Doch ich stehe total auf dem Schlauch.

P.S. Vektorrechnung oder ähnliches hatten wir noch nicht.

Comments

S1(-2/0)

S2(0/-4)

S3(4/0)

Du weisst bestimmt, wie man dem Umkreismittelpunkt eines Dreiecks (und den suchst du ja) konstruiert: Mittelsenkrechten miteinander schneiden.
Stelle also 2 lineare Funktionsgleichungen auf, die durch Seitenmittelpunkte gehen und senkrecht auf den Seiten stehen.
Wenn du das nicht kennst, skizzierst du nur die 3 Punkte und setzt irgendwo in die Mitte M(x|y), dann nimmst du den Pythagoras. Gesucht ist M(x|y)

nach Pythagoras gilt:

d1 = √((-2-x)^2 + (0-y)^2)

d2 = √((0-x)^2 + (-4-y)^2)

d3 = √((4-x)^2 + (0-y)^2)

Daraus 2 Gleichungen machen. Wenn du die Quadrate nimmst, sind die Wurzeln weg:

d1^2 = d2^2 und d2^2 = d3^2

Answer 1

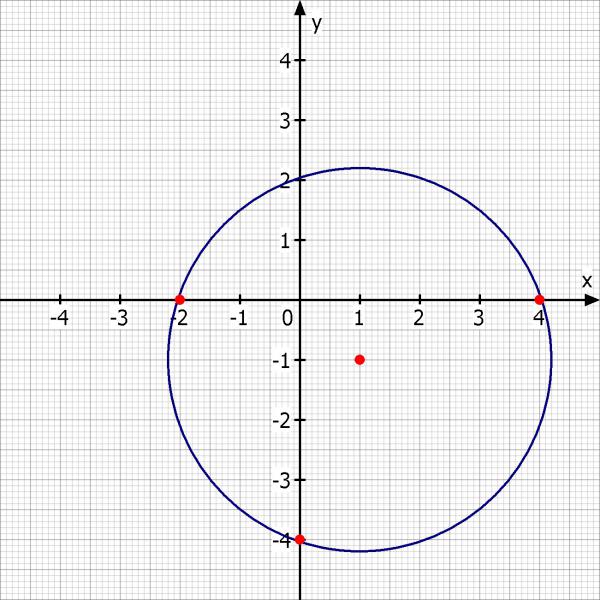
S1(-2/0), S2(0/-4), S3(4/0)

Stelle zwischen Zwei Punkten die Mittelsenkrechte aus. Hier besonders einfach

 

Mittelsenkrechte von S1 und S3

x = (-2 + 4) / 2 = 1

Jetzt noch die Mittelsenkrechte von S2 und S3

M = 1/2 * ([0, -4] + [4, 0]) = [2, -2]

m = (y1 - y2) / (x1 - x2) = (-4 - 0) / (0 - 4) = -4/-4 = 1

Senkrecht dazu -1

y = -1 * (x - 2) - 2 = -x

Mit x = 1 ergibt sich also y = -1

 

Der Punkt [1, -1] ist von allen 3 Punkten gleich weit entfernt.

Skizze:

Answer 2

\(S_1(-2|0)\)     \(S_2(0|-4)\)     \(S_3(4|0)\)  als Mittelpunkte von Kreisen:  Alle r müssen gleich lang sein.

1.) \((x+2)^2+y^2=r^2\)

2.) \(x^2+(y+4)^2=r^2\)

3.) \((x-4)^2+y^2=r^2\)

1.) mit 3.) :

\((x+2)^2+y^2=(x-4)^2+y^2\)

\((x+2)^2=(x-4)^2\)

\((x+2)^2-(x-4)^2=0\)

3.Binom:

\([(x+2)+(x-4)]*[(x+2)-(x-4)]=0\)

\([2x-2]*[-2]=0\)   \([2x-2]=0\) →   \(x=1\) 

1.) mit 2.) :

\((x+2)^2+y^2=x^2+(y+4)^2\)

\((1+2)^2+y^2=1^2+(y+4)^2\)

\(9+y^2=1^2+y^2+8y+16\)

\(9=1+8y+16\)  →  \(y=-1\) und \(x=1\)  → \(M(1|-1)\) einsetzen in 2.) \(1+(-1+4)^2=r^2\) →  \(r^2=10\)

Kreis, der durch durch die 3 Punkte geht:

\((x-1)^2+(y+1)^2=10\)