zu a)
Ich quadriere die Wurzelgleichung.
1/a² + 1/(a²•e)² = 4
1/a² + 1/(a^4•e²) = 4 |•a^4
a² + 1/e² = 4 a^4
a^4 -¼a² -1/(4e²) = 0
\( a^2={\frac{1}{8}\pm\sqrt{\frac{1}{64}+\frac{1}{4 e^{2}}}} \)
...
\(a=\pm \sqrt{\frac{1}{8}+\sqrt{\frac{1}{64}+\frac{1}{4 e^{2}}}} \)
\(a\approx\pm 0.5894 \)
zu b)
Falls die Ortskurve der Extrema gesucht ist:
g(x) = -x²/e
Falls das Minimum von f der Scheitelpunkt der Parabel p sein soll:
Scheitelpunktform
p(x) = b(x+1/a)² - 1/(a²e)
p(0)=0=b/a² -1/(a²e) → b=1/e
p(x)=1/e • (x + 1/a)² - 1/(a²e)
Ausmultipliziert:
p(x) = x²/e +2x/(ae)
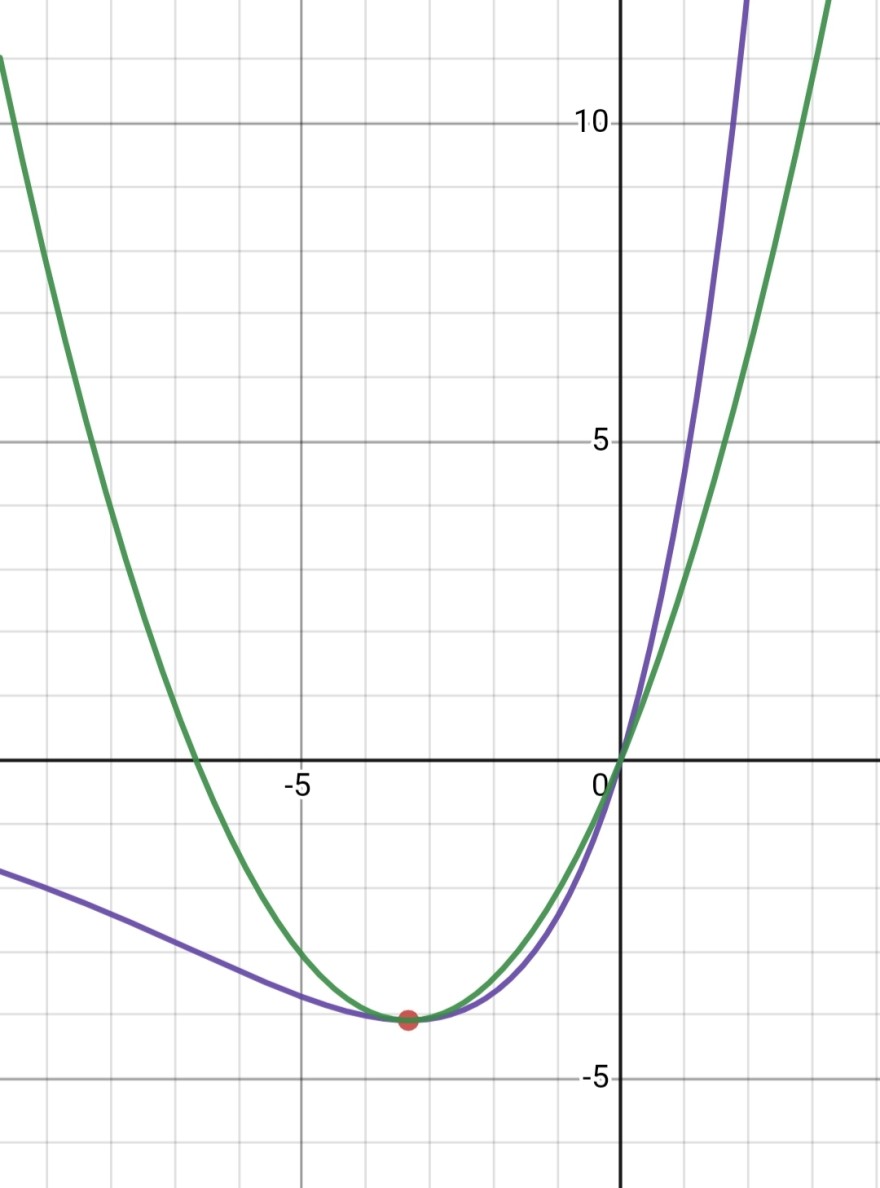
Violett f(x) für a=0,3
Grün p(x) für a=0,3