Wie hoch ist die Wahrscheinlichkeit, dass er heute Nacht Binge Watched?

Question

Aufgabe:

Every night, Jeremiah watches a TV show to relax. \( 80 \% \) of the time, he chooses to watch Manhanttan Eight-Six but \( 20 \% \) of the time, he chooses to watch Tickling Adam. Unfortunately, \( 20 \% \) of the time he ends up binge-watching the show until dawn. \( 40 \% \) of binges happen when he watches Manhanttan Eight-Six and \( 60 \% \) of binges happen when he watches Tickling Adam.
(A) What is the probability that he binges Manhattan Eight-Six tonight?
(B) Given that he is watching Manhattan Eight-Six tonight, what is the probability that he will binge it?
(C) What is the probability that he binges either tonight or tomorrow night (or both)?
(D) Given that he binges either tonight or tomorrow night (or both), what is the probability that he is watching Manhattan Eight-Six tonight?
(E) Given that he is watching Manhattan Eight-Six tonight, what is the probability that he binges either tonight or tomorrow night (or both)?
(F) Given that he binges Manhattan Eight-Six either tonight or tomorrow night (or both), what is the probability that he binges on both nights?

Problem/Ansatz:

… Vierfeldertafel

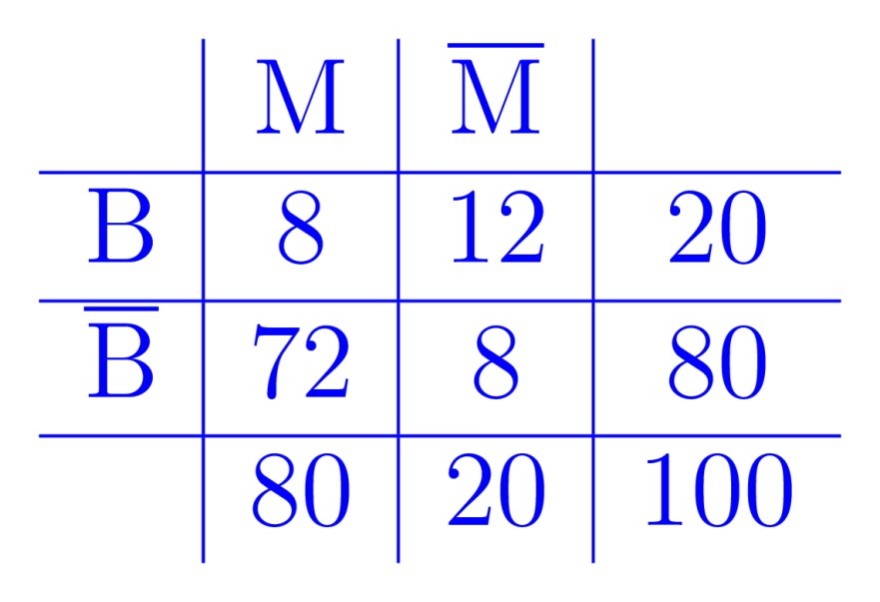
a) 8%
b) 8/80 = 10%
c) 0.8 * 0.2 + 0.8 * 0.2 + 0.2 * 0.2 = 36%

Könnte bei d) - f) Hilfe gebrauchen.

Comments

Möchtest Du das wissen was im Titel steht, oder das was in der Aufgabe steht?

---

Erstmal meinen Glückwunsch. Das, was du bisher gemacht hast, ist richtig.

Verwende bei d) bis f) den Satz von Bayes, für die bedingte Wahrscheinlichkeit

P(A | B) = P(A ∩ B) / P(B)

D.h. die Wahrscheinlichkeit, die du gerade unter c) berechnet hast, ist auch schon Teil der Rechnung für d).

---

P(A | B) = P(A ∩ B) / P(B)

Das ist aber nicht der Satz des Bayes, sondern die Formel für die bedingte Wahrscheinlichkeit..

An der Stelle kann ich Ihnen wieder nur den Spiegel vor dem Kopf halten:

Also bitte auch mal die Grundlagen auf dem Wikipedia Artikel lesen und nicht nur eine gepostete Formel anwenden ohne sie zu verstehen.

https://de.wikipedia.org/wiki/Satz_von_Bayes

---

Wo du gerade Wikipedia ansprichst

$$P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)} = \frac{P(A \cap B)}{P(B)}$$

Der Satz von Bayes und die bedingte Wahrscheinlichkeit ist die gleiche Formel.

Deine Beiträge werden echt peinlich. Wenn du jemanden korrigieren möchtest, dann solltest du bitte sicherstellen, dass das, was du schreibst, auch richtig ist.

---

Der Satz von Bayes und die bedingte Wahrscheinlichkeit ist die gleiche Formel.

Falsch, der Satz von Bayes folgt aus der Definition der bedingten Wahrscheinlichkeit.

Der Satz folgt unmittelbar aus der Definition der bedingten Wahrscheinlichkeit. (Wikipedia)

Das heißt nicht, dass die Formel für bedingte Wahrscheinlichkeit und der Satz des Bayes die gleiche Formel sind. Das würde auch jeder Mathe Professor bestätigen und zahlreiche Internetquellen. Sie stehen mit ihrer falschen Ansichtsweise mal wieder ganz alleine da.

Also wenn sich jemand peinlich macht, dann sind Sie das mit jedem weiteren Beitrag...

---

Ja. Du hast recht. Unser Prof. hatte das damals als Herleitung notiert.

Satz von Bayes

$$P(A \mid B)=\frac{P(A \cap B)}{P(B)}=\frac{P(B \cap A)}{P(B)}=\frac{P(B \mid A) \cdot P(A)}{P(B)}$$

Hier war offensichtlich nur der Multiplikationssatz angewendet worden.