Aufgabe: Bestimmen Sie einen Vektor N ∈ R3 der Länge |N| = 1, der senkrecht auf E steht
E = (-1,-1,2) + a (0,1,0) + b (3,2,-1)
Problem/Ansatz:
Das Problem ist nun folgendes. Den Vektor N sollte ich meines Erachtens richtig ermittelt haben.
Kreuzprodukt der Richtungsvektoren bilden, dann auf die Länge 1 kürzen.
Was in diesem Fall sein sollte: (0,1,0) x (3,2,-1) = (-1,0,-3), auf die Länge eins gerechnet dann 1/√(10)*(-1,0,-3).
Nun sollen wir das ganze aber noch in Geogebra zeichnen, gesagt getan, aber nun das Problem.
Der Vektor liegt nicht senkrecht zur Ebene und ich habe absolut keine Ahnung wieso, weshalb und warum.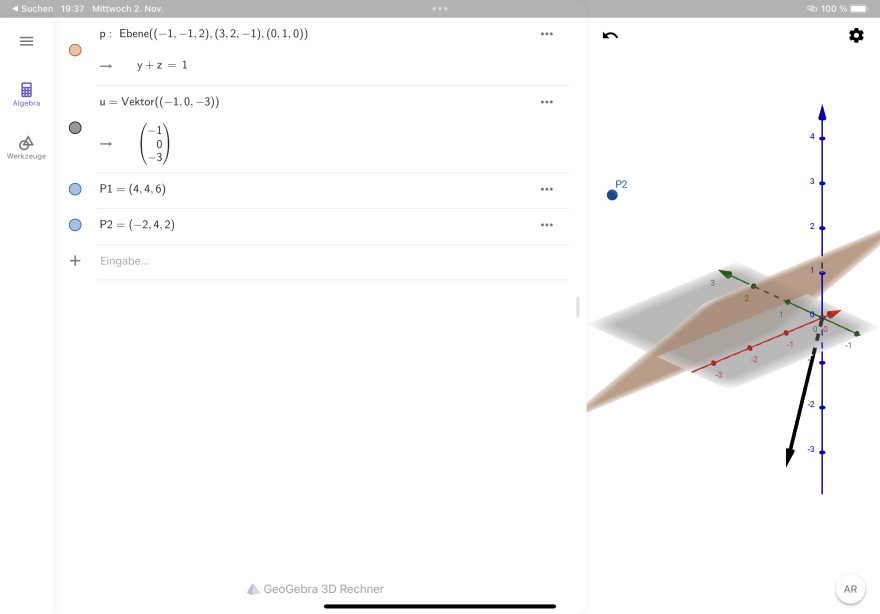
Text erkannt:
4 Suchen \( 19: 37 \) Mittwoch 2. Noy.