Die Punkte für Tangente bestimmen

Question

Aufgabe:

Bestimme für welche zwei Punkte auf der Parabel zu f(x)=4x^2 die Tangente an f durch den Punkt (1,-32) führt

Der Punkt mit dem kleinerem x-Wert:
der andere Punkt :

Problem/Ansatz

Wie kommt man auf die Lösung?

Answer 1

Wie kommt man auf die Lösung?

Die Steigung der Geraden durch die beiden Punkte (x | f(x)) und (1 | -32) ist dort gleich der ersten Ableitung von f.

Comments

Der Satz in der Antwort in Form einer Gleichung:

\(\begin{aligned} \frac{-32-4 x^{2}}{1-x}&=\frac{\partial}{\partial x} 4 x^{2} \\\\ \Longleftrightarrow \quad \quad \quad \quad x_{1}&=-2\\x_{2}&=4 \end{aligned}\)

Parabel blau eingezeichnet, die beiden Tangenten, die sich im Punkt (1 | -32) schneiden und die Parabel an den ausgerechneten Stellen berühren, gelb und grün:

Answer 2

Hallo,

mit der Punkt-Steigungsform kannst du die Gleichung der Tangenten an einer Stelle a so darstellen:

\(t(x)=f'(a)\cdot (x-a)+f(a)\)

Hier also \(t(x)=8a\cdot (x-a)+4a^2\)

Setze dann die Koordinaten von P in die Gleichung ein und löse nach a auf.

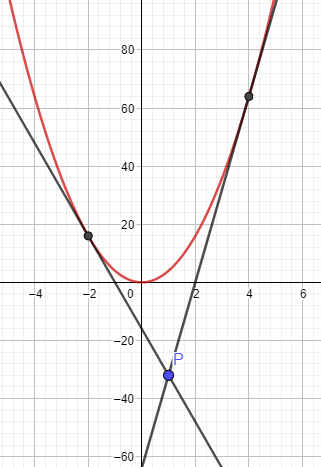
\(-32=8a\cdot (1-a)+4a^2\Rightarrow x_1=-2\quad x_2=4\)

Gruß, Silvia