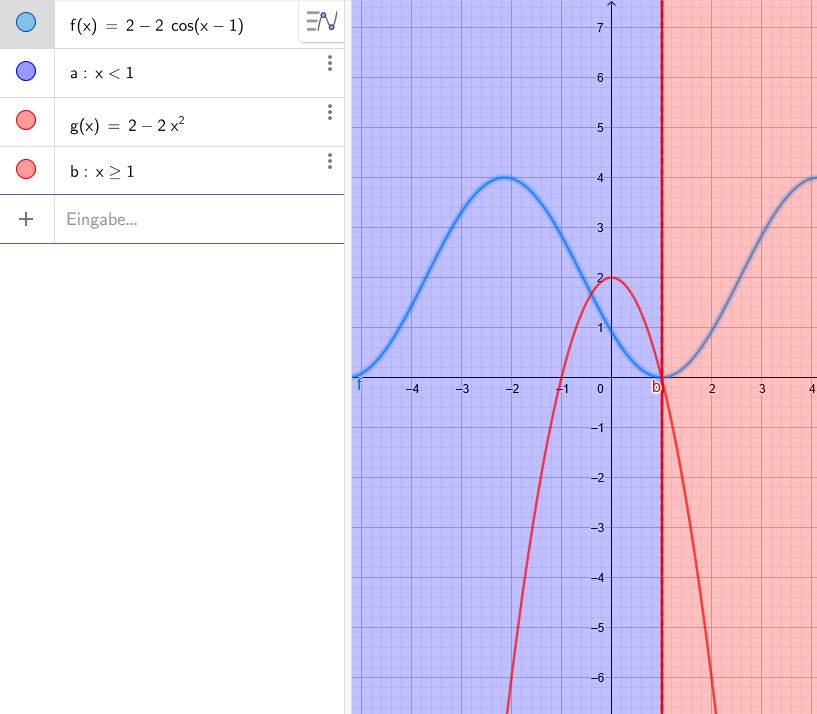
\(f(x)=\left\{\begin{array}{ll} 2-a \cdot \cos (x-1) & \text { für } x<1 \\ a-2 \cdot x^{2} & \text { für } x \geq 1 \end{array}\right. \)
\(2-a*cos(x-1)=a-2x^2\)
\(x=1\)
\(2-a*cos(1-1)=a-2*1^2\) \(2-a*cos(0)=a-2\)
\(2-a*1=a-2\) \(4=2a\) \(a=2\)
\(f(x)=\left\{\begin{array}{ll} 2-2 \cdot \cos (x-1) & \text { für } x<1 \\ 2-2 \cdot x^{2} & \text { für } x \geq 1 \end{array}\right. \)