f(x) = 2 - 8/x^7 = 0 --> x = 2^(2/7)
F(x) = 2·x + 4/(3·x^6)
A = ∫ (2^(2/7) bis 4) (2 - 8/x^7) dx = F(4) - F(2^(2/7)) = 24577/3072 - 7·2^(2/7)/3
Das Verhältnis der Teilflächen ergibt sich daher aus
q = (6145 - 7168·2^(2/7))/(7·(1024·2^(2/7) - 3511)) = 0.1637017390 : 1
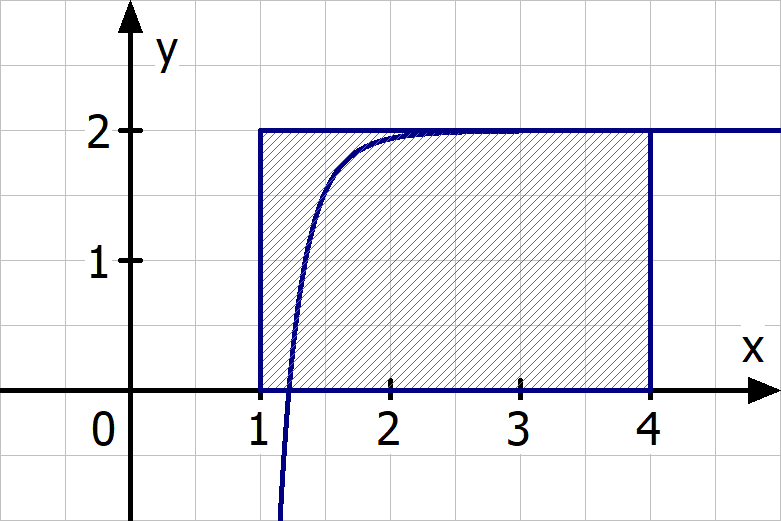
Skizze: