Aufgabe:
kommutativer Ring mit Addition ∧ und Multiplikation ∨?
Problem/Ansatz:
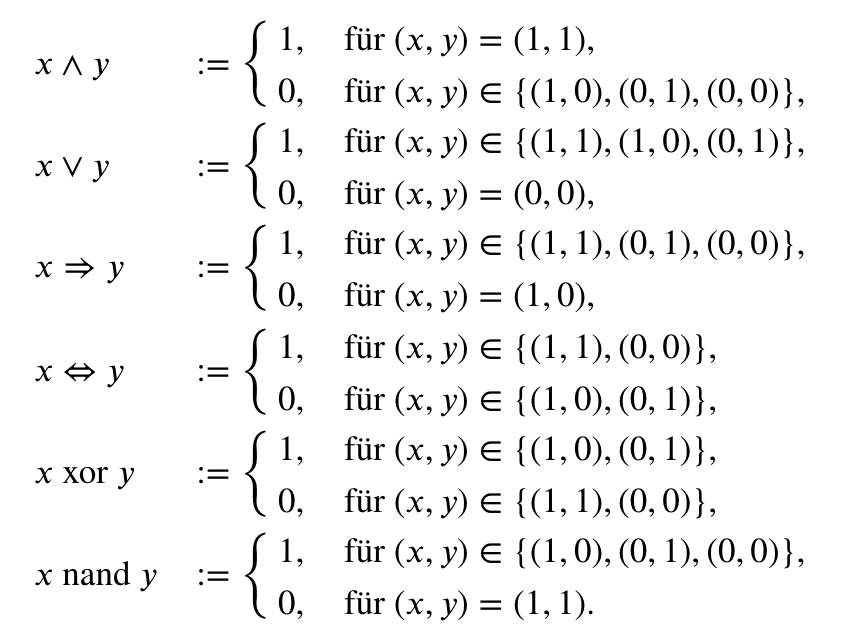
Text erkannt:
\( x \wedge y \quad:=\left\{\begin{array}{ll}1, & \text { für }(x, y)=(1,1), \\ 0, & \text { für }(x, y) \in\{(1,0),(0,1),(0,0)\},\end{array}\right. \)
\( x \vee y \quad:=\left\{\begin{array}{ll}1, & \text { für }(x, y) \in\{(1,1),(1,0),(0,1)\}, \\ 0, & \text { für }(x, y)=(0,0),\end{array}\right. \)
\( x \Rightarrow y \quad:=\left\{\begin{array}{ll}1, & \text { für }(x, y) \in\{(1,1),(0,1),(0,0)\}, \\ 0, & \text { für }(x, y)=(1,0),\end{array}\right. \)
\( x \Leftrightarrow y \quad:=\left\{\begin{array}{ll}1, & \text { für }(x, y) \in\{(1,1),(0,0)\}, \\ 0, & \text { für }(x, y) \in\{(1,0),(0,1)\},\end{array}\right. \)
\( x \) xor \( y \quad:=\left\{\begin{array}{ll}1, & \text { für }(x, y) \in\{(1,0),(0,1)\}, \\ 0, & \text { für }(x, y) \in\{(1,1),(0,0)\},\end{array}\right. \)
\( x \) nand \( y:=\left\{\begin{array}{ll}1, & \text { für }(x, y) \in\{(1,0),(0,1),(0,0)\}, \\ 0, & \text { für }(x, y)=(1,1) .\end{array}\right. \)
