Hallo,
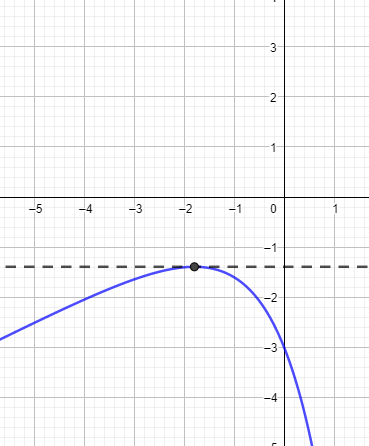
waagerechte Tangente bedeutet, es handelt sich um einen Extrem-, also Hoch- oder Tiefpunkt.
Um ihn zu berechnen, setzt du die 1. Ableitung = 0 und löst nach x auf.
Wenn du angeben sollst, ob es Maximum oder Minimum ist, setze dein Ergebnis in die 2. Ableitung ein.
Zur Bestimmung der y-Koordinate des Punktes setzt du dein Egebnis in die Ausgangsfunktion f(x) ein.
Gruß, Silvia