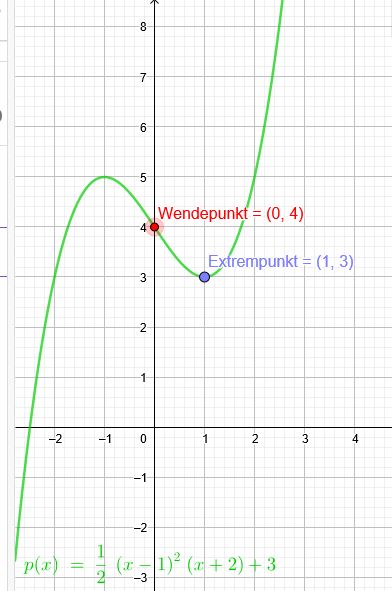
Der Punkt \(P(0|4)\) ist Wendepunkt, \(Q(1|3)\) ist Extrempunkt der Funktion \(f(x)\).
Ich verschiebe den Graphen von \(f(x)\) um \(3\) Einheiten nach unten
\(P(0|4)\) →\(P´(0|1)\) \(Q(1|3)\)→ \(Q´(1|0)\) ist doppelte Nullstelle
\(f(x)=a*(x-1)^2*(x-N)\)
\(P´(0|1)\):
\(f(0)=a*(0-1)^2*(0-N)=-a*N=1\) \(a=-\frac{1}{N}\)
Wendepunkt \(f´´(x)=0\)
\(f(x)=-\frac{1}{N}*[(x-1)^2*(x-N)]\)
\(f´(x)=-\frac{1}{N}*[(2x-2)*(x-N)+(x-1)^2]\)
\(f´´(x)=-\frac{1}{N}*[2*(x-N)+(2x-2)+2*(x-1)]\)
\(f´´(0)=-\frac{1}{N}*[2*(0-N)+(-2)+2*(0-1)=0]\) \(N=-2]\) \(a=\frac{1}{2}\)
\(f(x)=\frac{1}{2}*(x-1)^2*(x+2)\)
\(p(x)=\frac{1}{2}*(x-1)^2*(x+2)+3\)