Hallo, während meiner Prüfungsvorbereitung komme ich bei folgender Aufgabe nicht weiter und bitte um die Lösung:
Aufg. 3: Funktionen / Gleichungen / Ungleichungen
a) Bestimmen Sie den Definitionsbereich und berechnen Sie die Lösungsmenge der Gleichung
\( 2 \ln (x)=\ln (2-x)+\ln (1-x) \quad \) für \( x \in I R \).
b) Eine gebrochen-rationale Funktion \( f \) habe eine Polstelle bei \( x=5 \) und es gelte \( \lim \limits_{x \rightarrow \pm \infty} f(x)=-17 \). Außerdem verlaufe der Graph der Funktion durch den Punkt \( P=(7 ; 9) \). Geben Sie eine möglichst einfache Funktionsvorschrift mit genau diesen Eigenschaften an.
c) i) Welche Asymptote hat die Funktion \( f(x)=\frac{3 x^{2}-1}{x} \) für \( x \rightarrow \infty \) ?
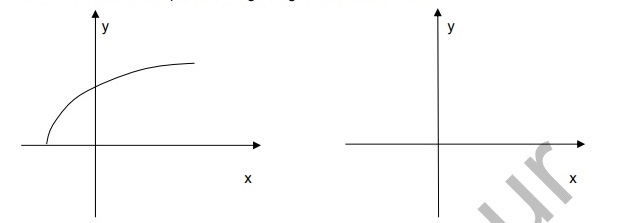
ii) In der linken Skizze ist der Graph der Funktion \( y=f(x) \) dargestellt.
Skizzieren Sie den Graphen der zugehörigen Umkehrfunktion.
Vielen Dank im Voraus für die Hilfe.
Liebe Grüße
Sevi