Berechnen Sie Bild (A) und ker(A) und argmin

Question

Aufgabe: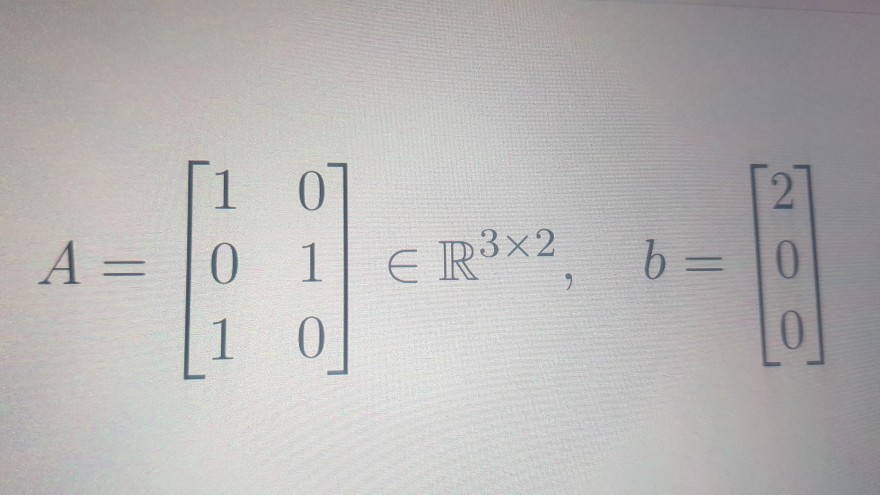

Der Rang von A ist 2.

1. Berechnen Sie Bild (A)

2. berechnen Sie Kern (A)

3. berechnen sie argmin x∈ℝ² IIb - AxII ²

4. verwenden Sie die 3 Aufgabe, um A+b zu berechnen. ( das Plus soll hier für das Zeichen der pseudo-inverse stehen)

Problem/Ansatz:

Hi vielleicht könnt ihr mir hier weiterhelfen. Ich weiß an sich wie man das Bild und den Kern von A berechnet und was das eigentlich bedeutet, aber irgendwie weiß ich es bei der Matrix nicht, weil sie ja nur aus 0 und 1 besteht.

Bei der dritten Ausgabe weiß ich leider nicht ganz, wie ich das Rechnen soll und die vierte kann ich deswegen auch nicht versuchen.

Vielen danke schonmal, ihr würdet mir wirklich helfen, dass ich das Thema besser verstehe.

Answer 1

1. \(\begin{pmatrix} 1 & 0 \\ 0 & 1\\1&0 \end{pmatrix}\cdot \begin{pmatrix} s  \\ t \end{pmatrix}=\begin{pmatrix} s \\ t\\s \end{pmatrix}=s\cdot \begin{pmatrix} 1  \\ 0 \\1\end{pmatrix}+t\cdot \begin{pmatrix} 0 \\ 1 \\0\end{pmatrix}\Rightarrow \)

\(Bild(A)=<\begin{pmatrix} 1  \\ 0 \\1\end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\0\end{pmatrix}>\)

2. \(Kern(A)=  <\begin{pmatrix} 0 \\ 0\end{pmatrix}>\)