Aufgabe:
Welche der Mengen sind Untervektorräume der angegebenen Vektorräume:
a) \( V_{1}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1}=2 x_{2}=3 x_{3}\right\} \subset \mathbb{R}^{3} \);
b) \( V_{2}=\left\{\left(x_{1}, x_{2}\right): x_{1}^{4}+x_{2}^{4}=0\right\} \subset \mathbb{R}^{2} \);
c) \( V_{3}=\left\{\left(\mu+\lambda, \lambda^{2}\right): \mu, \lambda \in \mathbb{R}\right\} \subset \mathbb{R}^{2} \);
d) \( V_{4}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1} \geq x_{2}\right\} \subset \mathbb{R}^{3} \);
e) die Lösungsmenge \( \mathrm{L} \subset C^{1}(\mathbb{R}) \) der Differentialgleichung \( y^{\prime \prime}(t)+t^{2} y(t)=e^{t} \).
Problem/Ansatz:
Also es muss ja geltn, das der Untervektorraum keine leere Menge ist, und Addition und Skalaremultiplikation möglich ist.
Ich bin da jetzt so ran gegangen, ist das richtig?
a)
b)

Text erkannt:
a) \( \quad V_{1}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1}=2 x_{2}=3 x_{3}\right\} \subset \mathbb{R}^{3} \)
1. Bedingung \( U \notin \phi \) exfillt, da der Nullvehtor Teil des Unterraumes ist.
2. Bedingung \( \left(\begin{array}{l}x \\ y \\ z\end{array}\right)+\left(\begin{array}{c}u \\ v \\ w\end{array}\right)=\left(\begin{array}{c}x \\ 2 x \\ 3 x\end{array}\right)+\left(\begin{array}{c}u \\ 2 u \\ 3 v\end{array}\right)=\left(\begin{array}{c}x+u \\ 2 x+2 u \\ 3 x+3 u\end{array}\right)=\left(\begin{array}{c}x+v \\ 2(x+u) \\ 3(x+v)\end{array}\right) \in V_{1} \)
3. Bedingung \( \lambda \cdot\left(\begin{array}{l}x \\ y \\ z\end{array}\right)=\lambda \cdot\left(\begin{array}{c}x \\ 2 x \\ 3 x\end{array}\right)=\left(\begin{array}{c}\lambda x \\ 2 \lambda x \\ 3 \lambda x\end{array}\right) \in V_{1} \)
\( \rightarrow \) ist ein Untervehtorraum des angegebenen Vehtorraums
b)
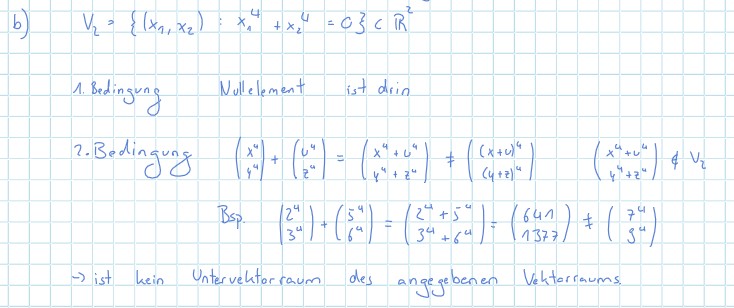
Text erkannt:
b) \( \quad V_{2}=\left\{\left(x_{1}, x_{2}\right): x_{1}^{4}+x_{2}^{4}=c\right\} c \mathbb{R}^{2} \)
1. Bedingung Nulelement ist drin
2. Bedingung \( \left(\begin{array}{l}x^{4} \\ y^{4}\end{array}\right)+\left(\begin{array}{l}u^{4} \\ z^{4}\end{array}\right)=\left(\begin{array}{l}x^{4}+u^{4} \\ y^{4}+z^{4}\end{array}\right) \neq\left(\begin{array}{l}(x+v)^{4} \\ (4+z)^{4}\end{array}\right) \quad\left(\begin{array}{l}x^{4}+u^{4} \\ y^{4}+z^{4}\end{array}\right) \notin v_{2} \)
Bsp. \( \quad\left(\begin{array}{l}2^{4} \\ 3^{4}\end{array}\right)+\left(\begin{array}{c}5^{4} \\ 6^{4}\end{array}\right)=\left(\begin{array}{l}2^{4}+5^{-4} \\ 3^{4}+6^{4}\end{array}\right)=\left(\begin{array}{c}641 \\ 1377\end{array}\right) \neq\left(\begin{array}{l}7^{4} \\ 9^{4}\end{array}\right) \)
\( \rightarrow \) ist kein Untervehtorraum des angegebenen Vehtarraums.
c)

Text erkannt:
c) \( \quad V_{3}=\left\{\left(\mu+\lambda_{1} \lambda^{2}\right): \mu_{1} \lambda \in \mathbb{R}\right\} \subset \mathbb{R}^{2} \quad\left(\begin{array}{c}\mu+\lambda \\ \lambda^{2}\end{array}\right) \)
1. Bedingung: Dee Untervehtorraum ist nicht leer, da das Nullelement teil des Raumes ist.
2. Bedingung: \( \quad\left(\begin{array}{c}x+y \\ y^{2}\end{array}\right)+\left(\begin{array}{c}z+w \\ w^{2}\end{array}\right)=\left(\begin{array}{c}x+y+z+w \\ y^{2}+w^{2}\end{array}\right)=\left(\begin{array}{c}(x+z)+(y+w) \\ y^{2}+w^{2}\end{array}\right) \neq\left(\begin{array}{c}(x+z)+(y+w) \\ (y+w)^{2}\end{array}\right) \) Bsp. \( \quad\left(\begin{array}{c}1+2 \\ 2^{2}\end{array}\right)+\left(\begin{array}{c}3+4 \\ 4^{2}\end{array}\right)=\left(\begin{array}{c}4+6 \\ 2^{2}+4^{2}\end{array}\right)=\left(\begin{array}{c}4+6 \\ 20\end{array}\right) \neq\left(\begin{array}{c}4+6 \\ 36\end{array}\right) \)
\( \rightarrow \) ist kein Untervehtorraum des angegebenen Vehtorraums.
d)

Text erkannt:
d) \( \quad V_{4}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1} \geq x_{2}\right\} \subset \mathbb{R}^{3} \)
1. Bedingeng Nollelement ist enthalten
2. Bedingung
\( \begin{array}{l} \left(\begin{array}{l} x \\ y \\ z \end{array}\right)+\left(\begin{array}{l} v \\ v \\ w \end{array}\right)=\left(\begin{array}{l} x+v \\ y+v \\ z+w \end{array}\right) \\ \text { da } x \geq y \quad 1+v \\ \text { mit } x \geq y \quad x \neq y \\ \end{array} \)
3. Bedingung
\( \begin{array}{l} \lambda \cdot\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{l} \lambda x \\ x y \\ \lambda z \end{array}\right) \quad \text { da } x \geq y \quad 1 \cdot \lambda \\ \text { mit } \lambda \geq 0 \\ \gamma\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{c} \gamma x \\ \gamma y \\ \gamma z \end{array}\right) \quad d a \quad x \geq y \quad 1 \cdot \gamma \\ \end{array} \)
mit \( \gamma<0 \)
\( \gamma x \leq \gamma y \rightarrow \) für \( x>y \) gilt \( \gamma x<\gamma y \)
\( \rightarrow \) nicht Teil des Veliforraums
\( \rightarrow \) ist kein Vektorraum des angegebenen Vektorraums
e), hier habe ich leider keine Idee, ich denke erstmal die DGL lösen, oder? Wie mache ich dann weiter?
Vielen Dank schonmal im Voraus.