Aufgabe: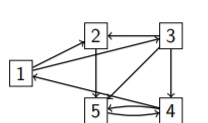
Die Skizze visualisiert exemplarisch 5 Internetseiten. Die Pfeile zeigen an, welche Webseiten aufeinander verweisen. Beispielsweise verweist die Website 1 auf 2 und 3. Das Ziel ist es, diese Webseiten sinnvoll nach ihrer Popularität zu ordnen, ihnen also ein Ranking zuzuweisen.
(a) Die Übergangsmatrix \( A=\left(a_{i j}\right) \in \mathbb{R}^{5 \times 5} \) fasst die Informationen der Grafik zusammen. Der Eintrag \( a_{i j} \) gibt die Wahrscheinlichkeit an für einen Übergang von der Webseite \( j \) auf die Webseite \( i \) an. Er ist definiert als 0 , falls kein Link von \( j \) nach \( i \) besteht, andernfalls als \( a_{i j}=(\#\{\text { ausgehende Links von } j\})^{-1} \). Die Schreibweise \#\{ ausgehende Links von j\} bezeichnet die Mächtigkeit der Menge \{ausgehende Links von \( j\} \), also die Anzahl an Elementen dieser Menge. Stellen Sie die Matrix \( A \) auf.
(b) Einer Webseite \( i \) kann nun ein Ranking \( x_{i} \) zugeordnet werden, indem man das Ranking der auf sie verweisenden Webseiten \( j \) mit den jeweiligen Übergangswahrscheinlichkeiten \( a_{i j} \) multipliziert und diese aufsummiert: \( x_{i}=\sum \limits_{j=1}^{5} a_{i j} \cdot x_{j} \). Überführen Sie diese Gleichungen in Matrixschreibweise und zeigen Sie, dass der gesuchte Vektor \( x \) im Eigenraum zum Eigenwert 1 liegt.
(c) Zeigen Sie, dass 1 ein Eigenwert der Matrix \( A \) ist.
(d) Berechnen Sie das gesuchte Ranking \( x \) der Webseiten.
Problem/Ansatz:
a) Ich habe folgende Matrix heraus:
\( \Rightarrow\left(\begin{array}{ccccc}0 & 0 & 0 & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & \frac{1}{3} & 0 & 0 \\ \frac{1}{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 / 3 & 0 & 1 \\ 0 & 1 & 1 / 3 & 1 / 2 & 0\end{array}\right) \)
b)
\( x_{1} \cdot\left(X_{1} \cdot 0+X_{2}\cdot 0+X_{3} \cdot 0+X_{4} \cdot \frac{1}{2}+X_{5} \cdot 0\right) \)
.......usw.
In Matrixschrwreibweise:
\( \left(\begin{array}{ccccc}0 & 0 & 0 & 1 / 2 & 0 \\ 1 / 2 & 0 & 1 / 3 & 0 & 0 \\ 1 / 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 / 3 & 0 & 1 \\ 0 & 1 & 1 / 3 & 1 / 2 & 0\end{array}\right)\left(\begin{array}{l}X_{1} \\ X_{2} \\ X_{3} \\ X_{4} \\ X_{5}\end{array}\right)=\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5}\end{array}\right) \)
Wie zeige ich, dass der gesuchte Vektor x im Eigenraum zum Eigenwert 1 liegt?
C) in A ist der EW zweimal bereits notiert in Form der Einheitsvektoren. (Spalte 2 und 5)
Da es der einzige Eintrag in der Spalte ist handelt es sich um einen EW.
d)muss ich da ein LGS machen mit (A||xi)?