Aufgabe:
Wir betrachten \( \mathbb{R}^{4} \) mit Standardskalarprodukt. Verwenden Sie ohne Beweis, dass die untenstehende Menge \( B \) eine Basis von \( \mathbb{R}^{4} \) ist.
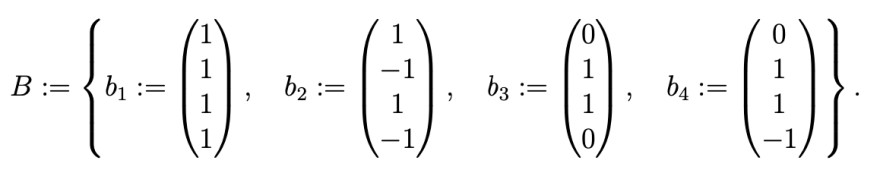
Text erkannt:
\( B:=\left\{b_{1}:=\left(\begin{array}{l}1 \\ 1 \\ 1 \\ 1\end{array}\right), \quad b_{2}:=\left(\begin{array}{c}1 \\ -1 \\ 1 \\ -1\end{array}\right), \quad b_{3}:=\left(\begin{array}{l}0 \\ 1 \\ 1 \\ 0\end{array}\right), \quad b_{4}:=\left(\begin{array}{c}0 \\ 1 \\ 1 \\ -1\end{array}\right)\right\} \)
a) Zeigen Sie, dass \( b_{1} \) und \( b_{2} \) orthogonal zueinander sind.
b) Bestimmen Sie eine Basis des orthogonalen Komplements \( \left(b_{3}\right)^{\perp} \) von \( b_{3} \).
c) Verwenden Sie die Gram-Schmidt-Orthonormalisierung, um aus \( B \) eine Orthonormalbasis von \( \mathbb{R}^{4} \) zu konstruieren.
Problem/Ansatz:
Ich habe hier leider keinen Ansatz, wie ich die Aufgabe lösen muss. Ich wäre über eine Lösung mit Erklärung sehr dankbar