Funktionsgleichung richtig berechnen

Question

Aufgabe:

Die gerade g5 hat die Funktionsgleichung y=1/3x +4. Die gerade g6 steht senkrecht auf g5 und verläuft durch den punkt P (-1/5)

Problem/Ansatz:

Meine Frage ist auf dem Punkt wird die Steigung mithilfe gleichsetzen berechnet ich verstehe aber nicht was Senkrecht bedeutet.

Answer 1

Hallo,

senkrecht aufeinander stehende Geraden erkennst du daran, dass die eine Steigung der negative Kehrbruch der anderen ist, oder anders gesagt

$\begin{array}{l}g_{1}: \;y=m x+t \\ g_{2}:\; y=n x+u \\[10pt] g_{1} \perp g_{2} \Leftrightarrow m=-\frac{1}{n}\end{array}$

bzw.

$g_{1} \perp g_{2} \Rightarrow \text{Steigung der senkrechten Geraden} \; m \cdot n=-1$

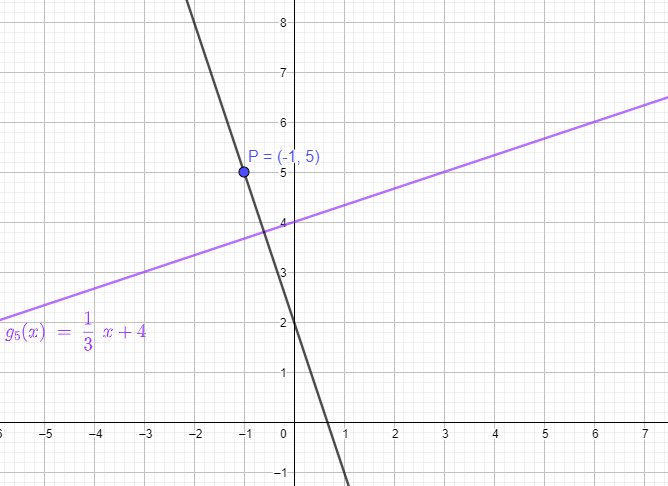
Damit kennst du die Steigung von $g_6$ und kannst sie mit den Koordinaten von P in die allgemeine Geradengleichung y = mx + n einsetzen, um n zu bestimmen.

Gruß, Silvia

Comments

Vielen Dank für die Antwort und Erklärung :).

Answer 2

Hallo,

was bedeutet Senkrecht: die zweite Gerade steht im rechten Winkel auf der ersten Gerade und geht durch den Punkt (-1|5)

sieht dann so aus.

Plotlux öffnen

f₁(x) = 1/2·x+4P(-1|5)f₂(x) = -2·x+3