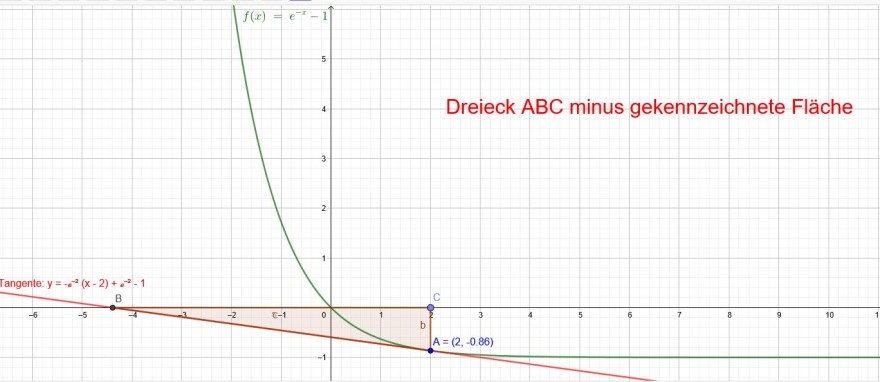
Berechne den Inhalt der Fläche, die vom Graphen von f, der Tangente im Punkt P und der x-Achse begrenzt wird.
a) \(f(x)=e^{-x}-1\) ; \(P(2|e^{-2}-1)\)
\(f´(x)=-e^{-x}\)
\(f´(2)=-e^{-2}\)
\( \frac{y-(e^{-2}-1)}{x-2} =-e^{-2}\)
Tangente:
\( y-e^{-2}+1 =-e^{-2}*(x-2)\)
\( y =-e^{-2}*(x-2)+e^{-2}-1\)
Schnitt mit x-Achse
\( -e^{-2}*(x-2)+e^{-2}-1=0\)
\( -e^{-2}*x+3*e^{-2}-1=0\)
\( e^{-2}*x-3*e^{-2}+1=0\)
\( e^{-2}*x=3*e^{-2}-1\)
\( x=3-\frac{1}{e^{-2}}\)