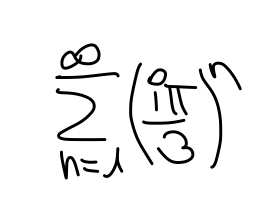Reihe mit komplexer Zahl auf Konvergenz prüfen - Rechenweg korrekt?

Question

Hallo zusammen, ich habe folgende Summe und möchte auf (absolute) Konvergenz oder divergenz prüfen.

Ich habe dies mit dem Wurzelkriterium geprüft und bekam π/3, da sich n noch zwei wegkürzt und i in Betrag gleich 1 ist. D.h die Reihe ist absolut divergent. Habe ich dies so richtig gemacht?

Ich komme nur nicht drauf wie ich Konvergenz prüfe, das wäre doch auch divergent? Denn es kommt immer π/3 raus (?)

Kann mir hierbei bitte jemand einen Tipp geben? Danke:)

Answer 1

Es ist \(|i\pi/3|>1\). Daher bilden die Reihenglieder keine

Nullfolge, d.h. die Reihe divergiert.

Comments

Ich danke dir, auf die Nullfolge hätte ich auch kommen können

Ist mein Vorgehen trotzdem korrekt?

---

Ja. So kannst du das machen. Ist aber ein bisschen mit

"Kanonen auf Spatzen geschossen" ;-)