Unteres Quartil und Varianz bestimmen

Question

Text erkannt:

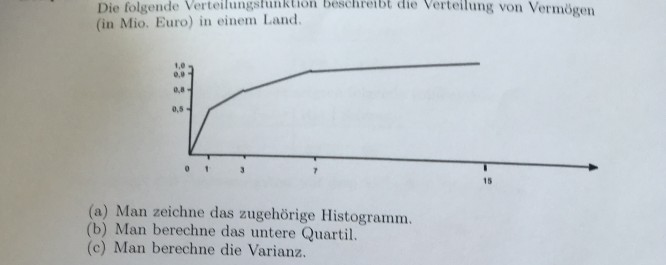
Die folgende Verteilungsfunktion beschretbt die Verteilung von Vermögen (in Mio. Euro) in einem Land.
(a) Man zeichne das zugehörige Histogramm.
(b) Man berechne das untere Quartil.
(c) Man berechne die Varianz.

Bei b und c bräuchte ich Hilfe. b ist ja Q(0,25) = n*p, 15*0,25= 3,75. Man muss ja bei nicht ganzzahligen abrunden und +1 dazurechnen und somit ist man bei 4. Man sollte aber auf 0,5 kommen. Und 4 entspricht ja der Wahrscheinlichkeit 0,1.

Und bei der Varianz habe ich Var(X)= E(X^2)-E(X) verwendt und komme auf 17,34, jedoch sollte man auf 10,73 kommen. Könnte mir jemand helfen?

Text erkannt:

Beispiel 1 (4 Punkte)
Die folgende Verteilungsfunktion beschreibt die Verteilung von Vermögen (in Mio. Euro) in einem Land.
(a) Man zeichne das zugehörige Histogramm.
(b) Man berechne das untere Quartil.
(c) Man berechne die Varianz.

Comments

Wo sind deine Probleme? Ich meine nen Histogramm zeichnen, werden wir dir hier jetzt nicht. Zur b) das untere Quartil ist das 0,25% Quantil, also du musst den jenigen Wert bestimmen, bei dem mindestens 25% der Daten unter dem Wert liegen.

---

Ja ich bin mir nicht sicher wie man hier das Quartil berechnet, sprich Q(25%)= n*p. Wäre das hier nicht 0,25*15=3,75. Es nicht ganzzahlig, dementsprechend muss man abrunden und n+1, also 4. Also an der 4. Stelle im Datenvektor. Aber wo sehe ich das hier in der Funktion

---

Naja in der Funktion schaust du auf die y-Achse und suchst den Wert 0,25 und bestimmt den entsprechenden x-Wert dazu, welcher dann dein unteres Quantil darstellt. Mehr ist es nicht :) dazu musst du natürlich sehen, dass der Abschnitt bis zur 1 durch eine lineare Funktion gekennzeichnet ist, ergo stell die Geradengleichung auf und setzte für deinen Funktionswert 0,25 ein. Ich weiß nucht wie tief ihr da begründen müsst, aber es ist durch die stetigkeit deiner Funktion klar, dass das Quartil eindeutig bestimmt ist.

---

Asoo ok, danke für die Erklärung. Und bzgl der Varianz hätte ich noch eine Frage. Für die Berechnung habe ich mir einfach die Wahrscheinlichkeitsfunktion hergenommen. Für P(x=1)=0,5 P(x=3)=0,3 P(x=7)=0,1, P(x=15)=0,1. Mit diesen Werten kann ich eben den Erwartungswert berechnen bzw. eben meine Varianz. Interpretiere ich etwas falsch?

---

Wenn die c) sich auf die im Bild dargestellte Verteilungsfunktion bezieht, dann kannst du nicht die Varianz so ausrechnen, denn die Zufallsvariable ist ja stetig und damit ist immer die Wahrscheinlichkeit fur eine exakte Stelle 0.

---

Das bedeutet schlussendlich: Ich würde natürlich auch die Formel E[X^2] - EX ^2 verwenden, aber du musst entsprechend Integrieren und zwar die Dichtefunktion*x^2 und einmal Dichte. * x für den Erwartungswert.

---

Ich weiß nicht, inwieweit ihr die Dichtefunktion gegeben habt, aber wenn nicht, wirst du nicht darum kommen die Verteilungsfunktion Abschnittsweise anzugeben und dann abzuleiten, um sie zu berechnen. Daher, dass die Verteilungsfunktion aus linearen Funktionen zusammengesetzt ist, sollte das gehen :)

---

Mh ok. Die Dichtefunktion ist aber nicht gegeben. Oder soll ich mir diese selbst herleiten?

---

Genau siehe meinen vorherigen Kommentar :)

---

Bitte beachte, dass du begründest, dass du sie differenzieren kannst auf dem offenen Intervall der einzelnen Abschnitte, achte darauf, dass du nicht an dem Punkt der Übergänge differenzieren kannst :)

Answer 1

b) Man berechne das untere Quartil.

Wie würdest du den das untere Quartil grafisch bestimmen. Würdest du nicht eine Horizontale y = 0.25 einzeichnen und die Stelle x bestimmen, an der der Graph der Verteilungsfunktion geschnitten wird?

Eigentlich denke ich, das könntest du zunächst machen und die Stelle grafisch näherungsweise ablesen.

Als Nächstes überlegst du dann, wie du diese Stelle auch rechnerisch bestimmen kannst. Schnittpunkt zweier linearer Funktionen ist auch nicht ganz so schwer.

Du solltest auch Aufgabe a) Man zeichne das zugehörige Histogramm nochmals machen. Ich vermute, du hast nicht bedacht, dass deine Dichtefunktion auf dem ganzen Intervall [0; 15] definiert ist. Das solltest du also berücksichtigen.