Exponentialverteilte Zufallsvariablen (Verteilungsfunktion)

Question

Hey, sehr ihr vielleicht, wie man damit auf das unterstrichene y kommt?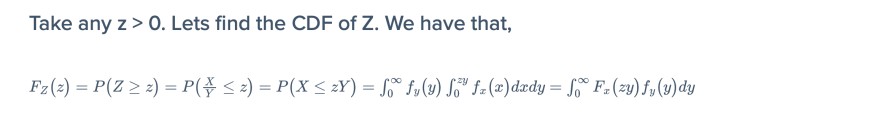

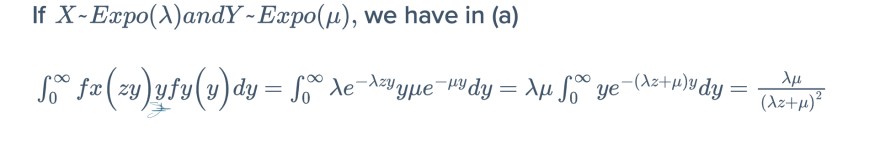
Irgendwie verstehe ich nicht, wieso nicht mit F_x(zy) weitergerechnet wurde, sondern in derm Beispiel mit den beiden exponentialverteilten Zufallsvariablen wieder die Dichte verwendet wurde und wie dieses zusätzliche y zustande kommt...:(

Ich wäre super dankbar, wenn mir hierbei jemand helfen könnte.

LG

Comments

Was wird denn da ausgerechnet. Was ist (a)? Ist beim allerersten Gleichheitszeichen ein Druckfehler P(Z >=z)?

---

Hallo, vielen Dank für den Hinweis. Hier ist die Aufgabe her: https://www.studysmarter.us/textbooks/math/a-first-course-in-probability-9th/jointly-distributed-random-variables/q65-if-x-and-y-are-independent-continuous-positive-random-va/

---

Die Idee ist eigentlich, dass Du Deine Frage einstellst, und nicht die Hilfswilligen aufforderst, sie selber zu suchen.

Aktuell kommt beim Link eine Fehlermeldung "504 Gateway Time-out". Wenn die Fehlermeldung gerade nicht kommt, dann sieht man keine Frage, sondern eine Antwort zu einer unbekannten Frage.

---

Hallo döschwo, es war definitiv nicht so angemacht, dass Leute die mir helfen möchten extra Arbeit bekommen. Tut mir leid, falls das so rübergekommen ist. Hintergrund des Links war eher, dass ich niemanden mit meiner Frage erschlagen/abschrecken möchte und ich vor allem nach der Rückfrage was a) genau ist, dachte, dass es am hilfreichsten wäre, wenn ich direkt meine ganze Quelle poste. a) war in diesem Fall die Berechnung von der Dichte von Z = X/Y.

Answer 1

Es geht also um die Dichte von \(Z=X/Y\). Dazu wird die Verteilungsfunktion differenziert. Natürlich kann man in diesem Fall auch einfach die Verteilungsfunktion F berechnen und daraus \(f=F'\) Oder man differenziert eben die Integraldarstellung von F. Das zusätzliche y tritt dann als innere Ableitung von \(zy\) nach z auf:

$$F'(z)=\partial_z \int_0^{\infty}dy f_Y(y)\int_0^{zy}dxf_X(x)=\int_0^{\infty}dy f_Y(y)\partial_z F_X(zy)=\int_0^{\infty}dy f_Y(y)f_X(zy)y$$

Comments

Vielen lieben Dank!:)