Extremalprobleme Hauptbedingung und nebenbedingung

Question

Aufgabe

Der größte Zylinder in einem geraden Kegel

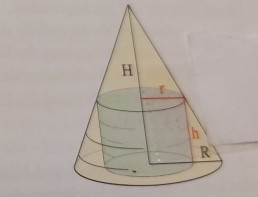
Ein gerader Kreiskegel hat den festen Radius \( \mathrm{R} \) und die feste Höhe \( \mathrm{H} \). Im Kreiskegel soll ein Zylinder mit dem Radius r und der Höhe h, so wie abgebildet, einbeschrieben stehen. Wie müssen die Zylindermaße \( r \) und \( \mathrm{h} \) gewählt werden, damit das Zylindervolumen \( \mathrm{V} \) maximal wird?

Hilfen: Zylindervolumen: \( \mathrm{V}_{\mathrm{ZYL}}=\pi \mathrm{r}^{2} \mathrm{~h} \)

Comments

Schau mal, ob dir diese Lösung hilft.

Answer 1

Strahlensatz (bzw. Verhältnisse in ähnlichen Dreiecken):

(H-h):r=H:R

Drücke damit r durch h oder h durch r aus.

Answer 2

Hallo

Hauptbedingung immer das was maximiert werden soll (oder minimiert) also hier das Volumen des Zylinders,

Nebenbedingung hier : es muss in den Kegel mit festen H und R passen, die Zeichnung zeigt wie mit Strahlensatz H,R und r, h zusammenhängen daraus dann den Zusammenhang zwischen r,h (der das feste R,H enthält )

Gruß lul

Answer 3

\(V(u)=u^2*π*(-\frac{H}{R}*u+H) \) soll maximal werden.
u.s.w.