Bestimme mit Hilfe der Symmetrieachse den Scheitelpunkt und gib die Funktionsgleichung an

Question

Aufgabe:

Die verschobene Normalparabel p geht durch die Punte P(-3|1) und Q(-1|1), die auf gleiche Höhe liegen. Bestimme mithilfe der Symmetrieachse den Scheitelpunkt und gib die Funtionsgleichung an „

Problem/Ansatz:

Answer 1

Bestimme mithilfe der Symmetrieachse den Scheitelpunkt und gib die Funtionsgleichung an.

Die Symmetrieachse liegt bei x = 1/2 * ((-3) + (-1)) = -2

Damit lautet die Funktionsgleichung der verschobenen Normalparabel bereits

f(x) = (x - (-2))² + e = (x + 2)² + e

Jetzt benutzt man einen Punkt um e zu ermitteln

f(-3) = (-3 + 2)² + e = 1 → e = 0

Und damit kann dann die Funktion aufgestellt werden.

f(x) = (x + 2)² + 0 = (x + 2)²

Comments

Man sollte es vlt. in Worten sagen:

Der Scheitel muss in der Mitte von -3 und -1 liegen, weil x= -3 und x= -1

dieselben Funktionswerte haben.

Wenn man das nicht bemerkt, wirds für manchen problemtisch beim Ansatz.

Daher wurde wohl noch explizit dazugesagt: auf gleicher Höhe

---

Danke ggT22, dass du den Sachverhalt nochmals für die Leute erklärt hast, die Probleme mit dem Begriff Symmetrieachse haben.

---

vielen Dank Der_Mathecoach für die gute Erklärung. Jetzt verstehe ich es.

Answer 2

Aloha :)

Willkommen in der Mathelounge... \o/

Die verschobene Normalparabel geht durch $P(-3|1)$ und $Q(-1|1)$.

Wenn wir die gesuchte Parabel um eine Einheit nach unten verschieben, werden die Punkte $P\to P'(-3|0)$ und $Q\to Q'(-1|0)$ zu Nullstellen. Wir geben also die Parabel mit den Nullstellen $x_1=-3$ und $x_2=-1$ an und verschieben diese danach wieder um eine Einheit nach oben:$$f(x)=(x+3)\cdot(x+1)+1$$Das können wir durch Ausrechnen noch weiter vereinfachen:$$f(x)=x^2+4x+4=(x+2)^2$$

Plotlux öffnen

f₁(x) = (x+3)·(x+1)+1P(-3|1)P(-1|1)Zoom: x(-5…1) y(-1…5)

Comments

Vielen Dank für die Antwort, aber ich verstehe nicht ganz, kannst du noch mal die Lösung geben wenn P(1|-1) und Q(-7|-1) sind, damit ich besser verstehe. Vielen Dank!

---

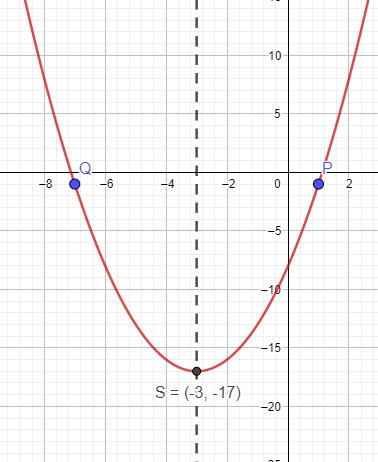
Die Scheitelpunktform einer verschobenen Normalparabel lautet

$f(x)=(x-d)^2+e$ und der Scheitelpunkt S hat die Koordinaten (d | e)

Die Symmetrieachse ist bei x = -3, also

$f(x)=(x+3)^2+e$

Um e zu bestimmen, setzt du die Koordinaten von P oder Q in die Gleichung ein. Ich nehme P.

$-1=(1+3)^2+e\\ -1=16+e\\ -17=e$

Somit lautet die Funktionsgleichung $f(x)=(x+3)^2-17$

---

Hallo Silvia.

Schade, dass du deinen richtigen Lösungsansatz nicht als selbständige Antwort hingeschrieben hast. Denn du verwendest im Gegensatz zu Tschakabumba tatsächlich die Symmetrieachse so wie es vermutlich von der Lehrkraft gemeint war.

---

Hey Coach, es reicht ja, wenn du das gemacht hast.

---

Die Symmetrieachse ist bei x = -3

Hallo Sylvia,

die SA ist x = -2

---

Mit den Punkten P(1|-1) und Q(-7|-1) kommt Silvia folgerichtig auf die Symmetrieachse von x = -3.

---

Trotzdem sollte zwei verschiedene Ergebnisse nicht ohne jeden Hinweis stehenbleiben!