Begründen Sie, dass das Dreieck DEP gleichschenklig ist, und bestimmen Sie die

Question

Aufgabe:

In einem kartesischen Koordinatensystem gilt für die Lage einiger der genannten Punkte: A(-5|5|0), B(-5|25|0), D(0|0|15), E(0|30|15), F(-25|5|15) und G(-10|10|35).
Eine Längeneinheit im Koordinatensystem entspricht 1 m in der Realität.

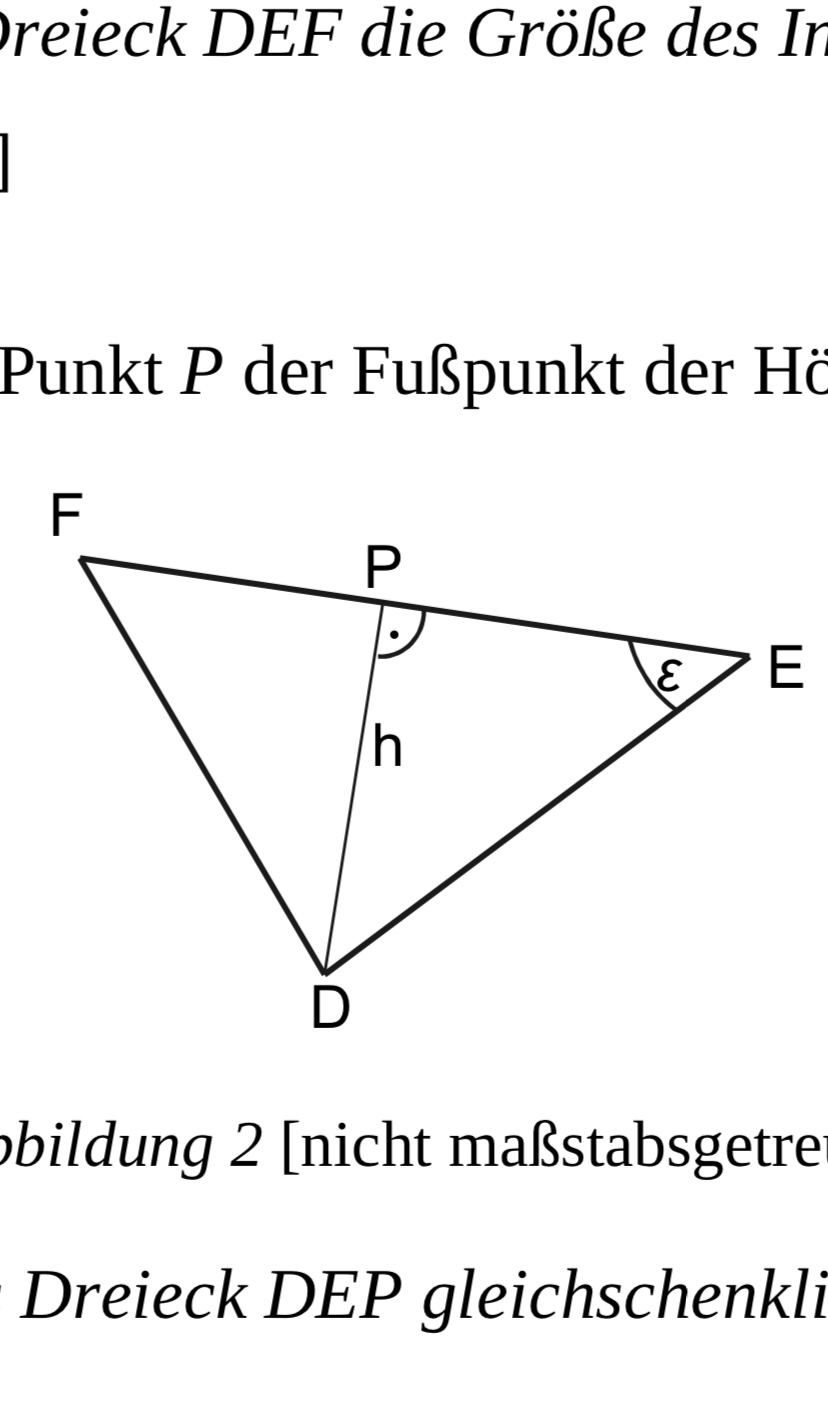
Begründen Sie, dass das Dreieck DEP gleichschenklig ist, und bestimmen Sie die
Länge der Höhe h.
[Zur Kontrolle: h = 15 Wurzel 2 ]

Problem/Ansatz:

Ich habe die länge der Seiten ausgerechnet, aber ich komme nicht darauf, dass es ein gleich Schenk leges Dreieck sein soll. Alle Seiten sind unterschiedlich lang.

P(-12,5|17,5|15)

|DE|= 30m

|DP|=21,5m

|PE|=17,6m

Text erkannt:

reieck DEF die Größe des Ir
Punkt \( P \) der Fußpunkt der
bildung 2 [nicht maßstabsgetre
Dreieck DEP gleichschenkl

Comments

Hallo,

P habe ich folgendermaßen berechnet:

OP=OD+0,5 EF

OP= (0 0 15) + 0,5 (-25 -25 0)

OP= (-12,5 -12,5 15)

Ist das richtig?

Answer 1

Wenn P der Fußpunkt des Lotes von D auf FE ist, dann hast du entweder P falsch oder DEP ist tatsächlich nicht gleichschenklig

Comments

Hallo,

P habe ich folgendermaßen berechnet:

OP=OD+0,5 EF

OP= (0 0 15) + 0,5 (-25 -25 0)

OP= (-12,5 -12,5 15)

Ist das richtig?

---

Dein Ergebnis für P ist falsch. Aber selbst wenn P richtig wäre, ist DEP nicht gleichschenklig. Das sieht man in einem Schnitt entlang der Ebene x₃=15;

---

Danke, wie berechnet man P denn?

---

Elementargeometrisch mit Hilfe meiner Skizze.

Löse das System

(1) \( \frac{x}{-25} \)+\( \frac{y}{30} \)=1 (Achsenabschnittsform)

(2) y= -\( \frac{5}{6} \)x (Senkrechte zu (1) durch den Ursprung).

Ergebnis P(\( \frac{-900}{61} \)|\( \frac{750}{61} \))