Auf einer Ferienfreizeit spielt der Betreuer Johannes mit den Kindern Linda, Peer und Nico mit einem Ball. Die Vier versuchen den Ball irgendwie über eine \( 8 \mathrm{~m} \) hohe Mauer zu bewegen (siehe Skizze - nicht maßstabsgetreul). Nicht alle Versuche gelingen. Sie diskutieren, worauf man achten muss, damit der Ball nicht "an der Mauer hängen bleibt" und notieren alle relevanten Daten.
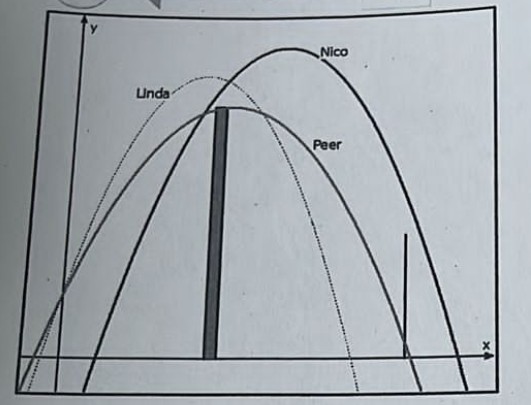
Die Flugkurve von Nicos Ball lässt sich durch die Funktion \( n(x)=-0,4 x^{2}+4,8 x-4,4 \) beschreiben
Nico meint, es sei am besten mit den Füßen zu schießen, eben wie beim Fußball. (Einheiten in \( \mathrm{m} \) ).
a) Die Mauer steht an der Stelle \( \boldsymbol{x}=4 \). Die Vierergruppe diskutiert, ob der Ball tatsächlich-wie in der Skizze - über die Mauer fliegen würde. Helfen Sie Ihnen.
b) Die Vier haben nur ein \( 6 \mathrm{~m} \) langes Maßband. Sie überlegen, wo der Ball landen würde und ob die Länge des Maßbandes ausreicht, um den Abstand des Landepunktes von der Mauer aus zu messen. Nico möchte zudem wissen, in welcher Entfernung von der Mauer er den Ball abgeschossen hat.
c) Um das Spiel etwas spannender zu machen, wird ein Smiley-Luftballon an einer Stange angebracht. Die Stange ist 5,5 \( \mathrm{m} \) von der Mauer entfernt, der Luftballon ist in einer Höhe von \( 4,6 \mathrm{~m} \) angebraucht und 30 cm hoch. Kann Nico den Luftballon treffen?
d) Jetzt möchten sie es genau wissen. In welcher Entfernung zur Mauer müsste die Stange aufgestellt werden, um den Smiley im oberen Bereich, also in \( 4,80 \mathrm{~m} \) Höhe zu treffen?
e) Peer wählt eine andere Methode, um den Ball über die Mauer zu bewegen. Er versucht es, indem er über Kopf wirft. Die Flugkurve seines Balls lässt sich durch \( \boldsymbol{p}(x)=-0,3(x-4,5)^{2}+8 \) beschreiben. Peer möchte wissen, welche maximale Höhe sein Ball erreicht und aus welcher Höhe der Ball abgeworfen wurde.
f) Peer und Nico möchten wissen, in welcher Entfernung von der Mauer beide Bälle dieselbe Höhe haben.
g) Linda versucht es ebenfalls, indem sie den Ball über den Kopf hebt und dann wirft. Nach einem Meter ha der Ball eine Höhe von \( 5,25 \mathrm{~m} \), nach \( 5 \mathrm{~m} \) eine Höhe von \( 8,25 \mathrm{~m} \). Der Ball landet nach \( 8 \mathrm{~m} \) auf dem Boden Wird der Ball über die Mauer fliegen?
Bestimmen Sie zunächst die Funktionsgleichung von Lindas Flugkurve und überprüfen Sie anschließend, der Ball über die Mauer fliegt.