
Text erkannt:
Antwort: 35 Jahre
A: 8 Jahre
(8) a) habjärlicher Verzinsung:
\( \begin{array}{c} k_{n}=k_{0}\left(1+\frac{p}{m \cdot 100}\right)^{n \cdot m} \\ 1040,67=1000\left(1+\frac{4}{6 \cdot 100}\right)^{1 \cdot 6} \end{array} \)
b) monaticher verzinsung:
\( \begin{aligned} k_{n} & =1000\left(1+\frac{4}{12 \cdot 00}\right)^{1 \cdot 12} \\ & \approx 1040,74 \end{aligned} \)
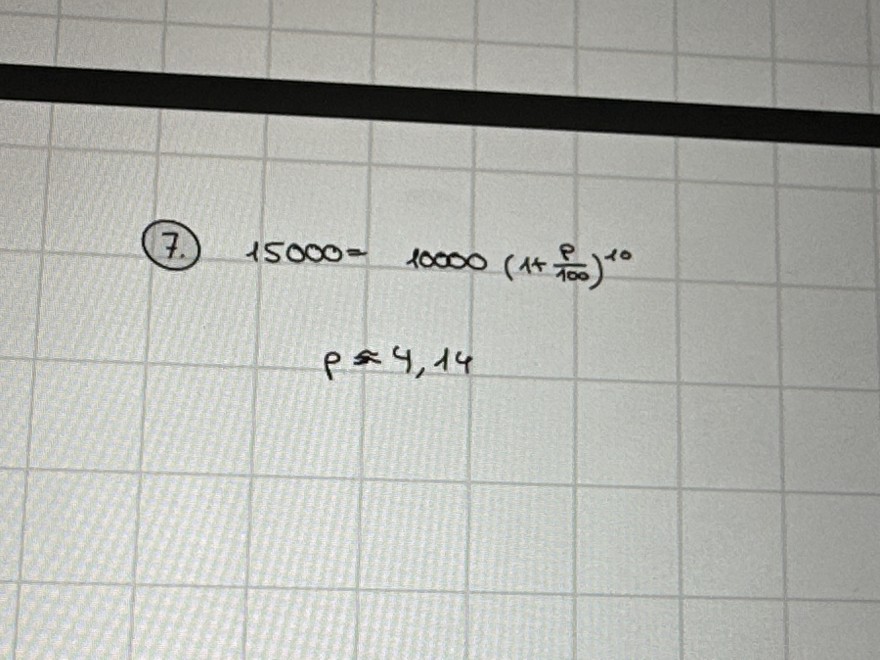
Text erkannt:
(7.) \( 15000=10000\left(1+\frac{P}{100}\right)^{10} \)
\( p \simeq 4,14 \)
Aufgabe:
Könnte jemand meine Aufgabe verbessern bzw. überprüfen ob diese richtig ist?
Aufgabe 7 und 8
Bitte überprüfen:
Text erkannt:
7. Sie möchten Ihr Geld so anlegen, dass in 10 Jahren aus 10000 Euro schließlich 15000 Euro werden. Welchen jährlichen Zinssatz muss Ihnen die Bank bieten? (Zinseszinsrechnung)
8. Ein Betrag von 1000 Euro wird zu \( 4 \% \) p.a. für ein Jahr angelegt. Berechnen Sie den Endbetrag
a.) bei halbjährlicher,
b.) bei monatlicher Verzinsung.
9. Gegeben sei ein Startkapital von 200 Euro.
Problem/Ansatz: