Vom Duplikat:
Titel: Anwendungsaufgabe mit e Funktion
Stichworte: ableitungen,e-funktion,stetigkeit
Aufgabe:…
In einem Freizeitpark soll eine Achterbahn gebaut werden. Der Verlauf des Endabschnitts der Achterbahn kann im Intervall (0;40] durch den Graphen der Funktion f(x) = (4x + 8)e °, 1235 dargestellt werden. Dabei gibt x die horizontale Länge und f(x) die Höhe des Endabschnittes der Achterbahn jeweils in m an.
a)Ermitteln Sie die maximale Höhe des Endabschnitts.
b) Wenn das maximale Gefälle größer als 40° ist, wird Kindern, die kleiner als 100cm sind, das Fahren der Achterbahn ohne Eltern nicht gestattet. Prüfen Sie, ob diese Bedingung im
Endabschnitt erfüllt ist.
)Berechnen Sie die durchschnittliche Steigung der Achterbahn auf dem Endabschnitt.
d) Weisen Sie nach, dass F(x) = (-32x-320)e^-0125x eine Stammfunktion von fist.
e) Die Seitenfläche des Endabschnitts wird beidseitig gestrichen. Berechnen Sie die Gesamtfläche, die gestrichen werden muss.
f)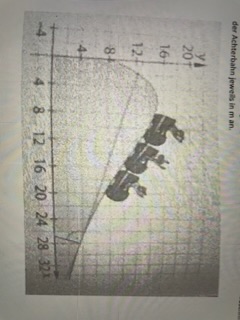 Aufgrund der Statik der Bahn muss eine Stütze aufgestellt werden, die an der Stelle x = 28 senkrecht zur Bahnkurve steht und am Boden verankert wird. Bestimmen Sie die Koordinaten des Punktes, an dem sich der Bodenpunkt der Stütze befindet, und geben Sie die Länge der Stützen an.
Aufgrund der Statik der Bahn muss eine Stütze aufgestellt werden, die an der Stelle x = 28 senkrecht zur Bahnkurve steht und am Boden verankert wird. Bestimmen Sie die Koordinaten des Punktes, an dem sich der Bodenpunkt der Stütze befindet, und geben Sie die Länge der Stützen an.