Wie lese ich k aus der Abbildung ab, um dann c anzugeben? Sigma/n-Umgebung

Question

Hallo,

Ich sag nur morgen ist Mathe-Abi...

Aufgabe:

Ein Hersteller von Fitnessarmbändern möchte für die Angabe einer Qualitätsgarantie

den Anteil fehlerhafter Fitnessarmbänder überprüfen. Der laufenden Produktion wird

eine Stichprobe vom Umfang 240 entnommen.

Die Auswertung des Stichprobenergebnisses erfolgt mithilfe des abgebildeten

Graphen, indem eine der Grenzen eines Prognoseintervalls für den unbekannten

Anteil fehlerhafter Fitnessarmbänder in der Stichprobe zu einer Sicherheitswahrscheinlichkeit

c ermittelt wird.

Für einen Wert k, k∈ℝ, k>0, ist der Graph der Funktion f mit

f(p) = p + k* \( \sqrt{\frac{p*(1-p)}{240}} \) und p∈[0;1] dargestellt.

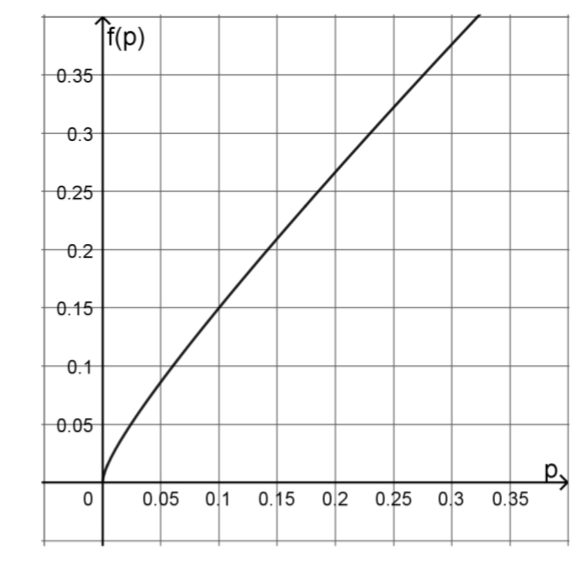
a) Ermitteln Sie mithilfe der Abbildung den Wert k und geben Sie eine mögliche

Sicherheitswahrscheinlichkeit c an.

b) Erläutern Sie die Bedeutung der bei der Auswertung des

Stichprobenergebnisses betrachteten Grenze des Prognoseintervalls.

Problem/Ansatz:

Ich denke, f(p) ist die obere Intevallsgrenze für ein Konfidenzintervall. Bei einer Sicherheitswahrscheinlichkeit von 68% müsste k=1 sein, bei 90% k=1,64, bei 95% k=1,96, bei 95,5% k=2, bei 99% k=2,58, bei 99,7% k=3.

Wie lese ich aber k aus der Abbildung ab, um dann c anzugeben?

Bei b) hätte ich gesagt, dass das Prognoseintervall auf der f(p)-Achse ist. Es bedeutet, dass der Anteil der fehlerhaften Fitnessarmbänder in der Stichprobe f(p) groß ist. Das heißt wenn man X/n bzw. X/240 rechnet, kommt man auf f(p)

Danke schon mal für eure Hilfe.

Answer 1

(a)

Du suchst nach einem Punkt auf dem Graphen von f, der gut ablesbar ist.

Der Graph von f enthält den Punkt \((p,f(p)) = (0.1,0.15)\). Damit gilt:

\(0.15 = 0.1+k\sqrt{\frac{0.1\cdot 0.9}{240}} \Rightarrow \boxed{k\approx 2.58}\)

Die Sicherheitswahrscheinlichkeit ist damit \(\boxed{c=99\%}\).

(b)

Da die Sicherheitswahrscheinlichkeit \(c=99\%\) beträgt, liegt der tatsächliche Anteil an fehlerhaften Bändern mit einer Wahrscheinlichkeit von ca. \(0.5\%\) oberhalb von \(f(p)\).