Hyperbolische Geraden beschreiben, im Inneren eines Winkels

Question

Aufgabe:

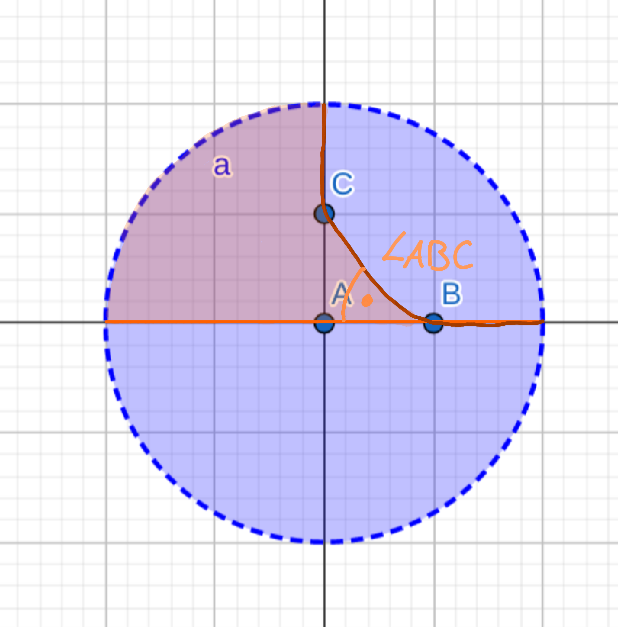
(b) Finden Sie (hyperbolische) Geraden g, die im inneren des Winkels verlaufen, \( \mathbf{g} \subset \operatorname{Int}(\angle \mathbf{A B C}) \).
Hinweis: Hyperbolische Geraden in \( \mathbb{D}^{2} \), die nicht durch 0 verlaufen, kann man als
\( \mathbf{g}=\left\{z \in \mathbb{D}^{2}:|z-m|^{2}=|m|^{2}-1\right\} \)
für ein \( m \in \mathbb{C}^{2} \) mit \( |m|^{2}>1 \) schreiben.

Problem/Ansatz:

Mir ist bewusst, wie die hyperbolischen Geraden verlaufen, aber ich verstehe den Hinweis nicht. Also wie ich die Geraden als Menge aufschreiben soll. Der markierte Bereich in Orange ist ja der Bereich, den wir untersuchen wollen, also ein Viertel des Kreises grob gesagt. Die hyperbolischen Geraden sind ja die, die senkrecht auf den Rand des Kreises aufkommen einfach gesagt.

Comments

Hallo

du suchst also Kreise, die senkrecht auf dem Viertelkreisradius stehen  wenn du einen  passenden Mittelpunkt m=z0 hast steht da die richtige Gleichung in der komplexen Ebene.

lul

Answer 1

Hallo

nimm 2 Punkte auf dem Viertel  Kreis, die Tangenten schneiden sich in dem Mittelpunkt m des gesuchten Kreises, der Radius  des Kreises ist dann r^2=|m|^2-1^2 ist dann wenn der  gegebene Kreis um 0  mit Radius 1 ist .

Gruß lul