Heyho liebe Freunde der Mathematik ich schreibe demnächst Klausur deswegen wäre es sehr geschickt wenn mir jemand das erklären könnte :D das vorliegende Dokument ist meine Rechnung und ich brauche eine Erklärung wie genau ich die Winkel der Halbachsen der Ellipse berechne. Das was ich dort in Sachen Winkel gerechnet habe ist mehr geraten als gerechnet um ehrlich zu sein deswegen bräuchte ich eine Erklärung hinsichtlich der Drehmatrix und wie man sie aus Ellipsen anwendet den Rest wie lange die Halbachse ist habe ich bereits fehlerfrei berechnet das ist nicht Relevant.
Vielen Dank im Voraus!!!

Text erkannt:
Aufgabe 1. Die Gleichung \( x^{2}-x y+y^{2}-6=0 \) beschreibt eine Ellipse in \( \mathbb{R}^{2} \). Bestimmen Sie die Richtung der Halbachsen und deren Länge.
\( \begin{array}{l} \underbrace{x^{2}-x y+y^{2}}-6=0 \\ a x^{2}+b x y+c y^{2}=0 \\ \Leftrightarrow(x, y) \cdot \underbrace{\left(\begin{array}{cc} 1 & -1 / 2 \\ -1 / 2 & 1 \end{array}\right)}_{=: A} \cdot\left(\begin{array}{l} x \\ y \end{array}\right) \\ \Leftrightarrow(x, y) \cdot\left(\begin{array}{ll} a & b / 2 \\ b / 2 & c \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \end{array}\right)=0 \\ \end{array} \)
1) Eigenwerte von \( A \) bestimmen:
\( \begin{array}{l} \operatorname{det}\left(\lambda \cdot I_{2}-A\right)=0 \\ \Leftrightarrow \operatorname{det}\left(\left(\begin{array}{cc} \lambda & 0 \\ 0 & \lambda \end{array}\right)-\left(\begin{array}{cc} 1 & -1 / 2 \\ -1 / 2 & 1 \end{array}\right)\right)=0 \\ \Leftrightarrow \operatorname{det}\left(\begin{array}{cc} \lambda-1 & 1 / 2 \\ 1 / 2 & \lambda-1 \end{array}\right)=0 \\ \Leftrightarrow(\lambda-1)(\lambda-1)-\frac{1}{2} \cdot \frac{1}{2}=0 \\ \Leftrightarrow \lambda^{2}-2 \lambda+1-1 / 4=0 \\ \Leftrightarrow \lambda^{2}-2 \lambda-3 / 4=0 \\ \lambda_{1 / 2}=-\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right)^{2}-3 / 4} \\ =1 \pm \sqrt{\frac{1}{4}} \\ =1 \pm \frac{1}{2} \\ \lambda_{1}=1+1 / 2=3 / 2 \quad \Rightarrow \lambda_{1}=\frac{3}{2} \\ \lambda_{2}=1-\frac{1}{2}=1 / 2 \quad \Rightarrow \lambda_{2}=1 / 2 \\ \end{array} \)
\( \begin{aligned} & \left(A-\lambda_{1} I_{2}\right) \cdot \vec{v}_{1}=\overrightarrow{0} \\ \Leftrightarrow & \left(\left(\begin{array}{cc} 1 & -1 / 2 \\ -1 / 2 & 1 \end{array}\right)-3 / 2 \cdot\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)\right) \cdot \vec{v}_{1}=\overrightarrow{0} \\ \Leftrightarrow & \left(\begin{array}{cc} -1 / 2 & -1 / 2 \\ -1 / 2 & -1 / 2 \end{array}\right) \cdot \vec{v}_{1}=\overrightarrow{0} \\ \Leftrightarrow & {\left[\begin{array}{cc|c} -1 / 2 & -1 / 2 & 0 \\ -1 / 2 & -1 / 2 & 0 \end{array}\right] z_{2}-z_{1} } \\ \Leftrightarrow & {\left[\begin{array}{cc|c} -1 / 2 & -1 / 2 & 0 \\ 0 & 0 & 0 \end{array}\right] } \end{aligned} \)

Text erkannt:
1) \( -1 / 2 x_{1}-\frac{1}{2} x_{2}=0 \)
2)
\( 0=0 \)
\( \begin{array}{l} \Rightarrow v_{1}=\left(\begin{array}{c} -\alpha \\ \alpha \end{array}\right) \stackrel{\alpha=1}{\Rightarrow} \vec{v}_{1}=\left(\begin{array}{c} -1 \\ 1 \end{array}\right) \\ \end{array} \)
\( \begin{array}{l} \Rightarrow \vec{v}_{2}=\left(\begin{array}{l} \beta \\ \beta \end{array}\right) \stackrel{\beta=1}{\Rightarrow} \vec{v}_{2}=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \\ \end{array} \)
Normierung dec Eigenvehtoren:
\( \begin{array}{l} \left\|v_{1}\right\|_{2}=\sqrt{(-1)^{2}+1^{2}}=\sqrt{2} \\ \widetilde{v}_{1}=\frac{1}{\left\|v_{1}\right\|_{2}} \cdot v_{1}=\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{c} -1 \\ 1 \end{array}\right)=\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) \quad \Rightarrow \widetilde{v}_{1}=\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) \\ \left\|v_{2}\right\|_{2}=\sqrt{1^{2}+1^{2}}=\sqrt{2} \\ \widetilde{v}_{2}=\frac{1}{\left\|v_{2}\right\|_{2}} \cdot v_{2}=\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{l} 1 \\ 1 \end{array}\right)=\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) \quad \Rightarrow \widetilde{v}_{2}=\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) \end{array} \)
Text erkannt:
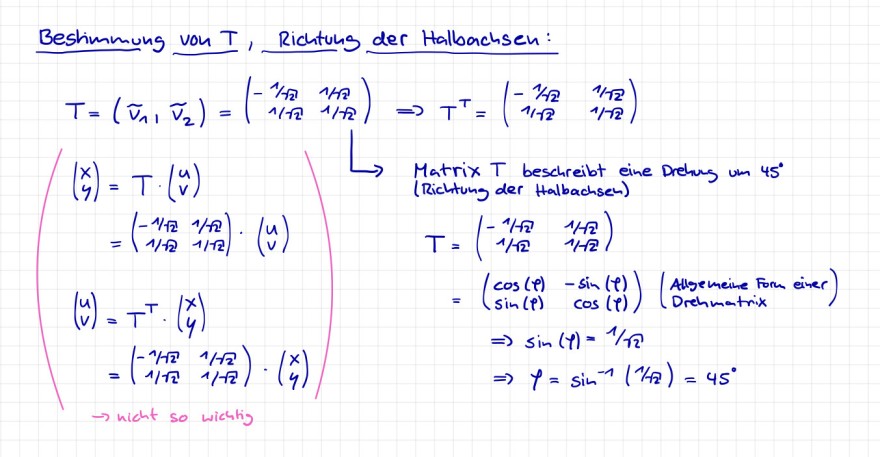
Beshmmung von \( T \), Richtung der Halbachsen:
\( \begin{array}{l} T=\left(\begin{array}{ll} \widetilde{v}_{1}, & \widetilde{v}_{2} \end{array}\right)=\left(\begin{array}{cc} -1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right) \Rightarrow T^{\top}=\left(\begin{array}{cc} -1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right) \\ \left(\begin{array}{l} x \\ y \end{array}\right)=T \cdot\left(\begin{array}{l} u \\ v \end{array}\right) \\ =\left(\begin{array}{cc} -1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 /-2 & 1 / \sqrt{2} \end{array}\right) \cdot\left(\begin{array}{l} u \\ v \end{array}\right) \\ \left(\begin{array}{l} u \\ v \end{array}\right)=T^{\top} \cdot\left(\begin{array}{l} x \\ y \end{array}\right) \\ \text { Matrix } T \text { beschreibt eine Drehung un } 45^{\circ} \\ T=\left(\begin{array}{cc} -1 /-\sqrt{2} & 1 /-2 \\ 1 / \sqrt{2} & 1 /-\sqrt{2} \end{array}\right) \\ =\left(\begin{array}{cc} \cos (\varphi) & -\sin (\varphi) \\ \sin (\varphi) & \cos (\varphi) \end{array}\right)\left(\begin{array}{l} \text { Allsemeine form einer } \\ \text { Drehmatrix } \end{array}\right) \\ \left.=\left(\begin{array}{cc} -1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \end{array}\right)\right) \\ \Rightarrow \sin (\varphi)=1 / \sqrt{2} \\ \Rightarrow \varphi=\sin ^{-1}(1 / \sqrt{2})=45^{\circ} \\ \end{array} \)
(Richtung der Halbachsen)
\( \rightarrow \) nicht so wichtis