Aufgabe:
a) Stelle die Stammfunktion F von f mit F (0)= 0 zunächst als Potenzreihe und dann als elementare Funktion dar.
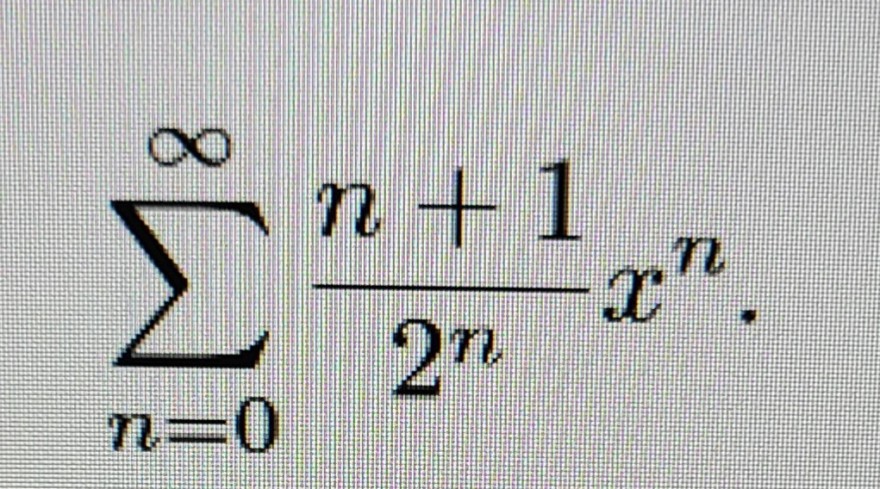
Text erkannt:
\( \sum \limits_{n=0}^{\infty} \frac{n+1}{2^{n}} x^{n} \)
b) Bestimme hieraus eine Darstellung von f als elementare Funktion.