Bestimmen Sie Pr[X = n] für alle n ∈ W_X.

Question

Ich habe folgende Aufgabe:

Man spielt folgendes Spiel. Es wird eine faire Münze so lange geworfen, bis Kopf
direkt nach Zahl geworfen wird. Die Zufallsvariable X beschreibt die Anzahl der Wurfe,
die hierfür benötigt werden. Der Wertebereich von X ist also W_X = {2, 3, . . .} = N\ {1}.

a) Bestimmen Sie Pr[X = n] für alle n ∈ W_X. Versuchen Sie dabei ein Muster in den
Wurfsequenzen zu erkennen, für die das Spiel nach genau n Würfen vorbei ist.

Antwort: hier habe ich die Dichte funktion verwendet und dann

f_X (n) = (1/2)ⁿ

stimmt das?

ich weiß jetzt aber nicht was für ein muster gemeint ist. ich hab die funktion mal in den funktionsplotter gegeben, wüsste aber nicht was ich damit anstellen könnte. Heißt das das die Wahrscheinlichkeit mit jedem X immer kleiner wird?

b) Berechnen Sie den Erwartungswert und die Varianz von X.
Hinweis: Sie dürfen verwenden, dass

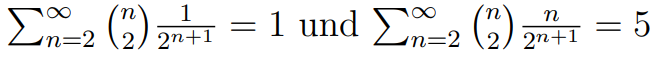
Text erkannt:

\( \sum \limits_{n=2}^{\infty}\left(\begin{array}{c}n \\ 2\end{array}\right) \frac{1}{2^{n+1}}=1 \) und \( \sum \limits_{n=2}^{\infty}\left(\begin{array}{l}n \\ 2\end{array}\right) \frac{n}{2^{n+1}}=5 \)

gilt

hier habe ich die Formel des Erwartungswerts hergenommen. Die muss man ja auch konvergenz prüfen. Meine Frage wäre. müsste es nicht von x = 2 bis nach n gehen? ich habe nicht wirklich eine Ahnung wie ich die Hinweise verwenden könnte.

Zu der Varianz habe ich keine Ahnung was ich mit der Formel für die Varianz machen könnte.

LG

Comments

Stelle mal alle Folgen von Kopf und Zahl auf, so dass das Spiel mit dem 4. Wurf endet. Dann, so dass das Spiel mit dem 5. Wurf endet. Dann schau mal, ob Du ein Muster erkennst.....

Answer 1

Versuchen Sie dabei ein Muster in den Wurfsequenzen zu erkennen, für die das Spiel nach genau n Würfen vorbei ist.

Für n = 2: ZK

Für n = 3: KZK, ZZK

Für n = 4: KKZK, KZZK, ZZZK

Für n = 5: KKKZK, KKZZK, KZZZK, ZZZZK

erkennst du schon was?

P(X = n) = (n - 1) * 0.5^(n - 2) * 0.5 * 0.5 = 0.5^n·(n - 1)