Stetigkeit von f untersuchen

Question

Aufgabe:

Sei f: ℝ² →ℝ mit

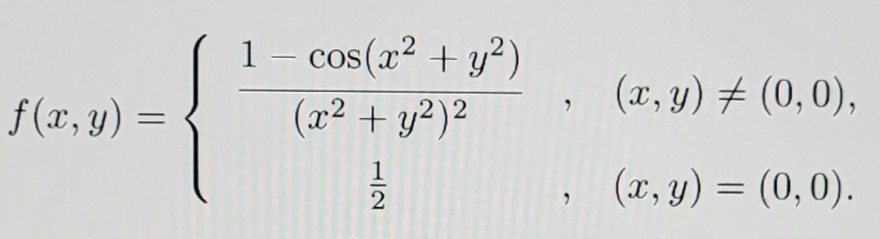
Text erkannt:

\( f(x, y)=\left\{\begin{array}{cl}\frac{1-\cos \left(x^{2}+y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}} & , \quad(x, y) \neq(0,0) \\ \frac{1}{2} & , \quad(x, y)=(0,0)\end{array}\right. \)

Untersuche f auf Stetigkeit

Comments

x=y=1/n. Was passiert für n gegen unendlich wenn du das einsetzt?

---

Dann ist der Grenzwert gleich 1/2, was aber nichts zur Lösung der Aufgabe beiträgt.

Answer 1

Übergang zu Polarkoordinaten liefert wegen \((x,y)\to (0,0)\iff r^2\to 0\),

wobei \(r^2=x^2+y^2\) ist: \(\lim_{r^2\to 0}\frac{1-\cos(r^2)}{r^4}\)

L'Hospital:

\(=\lim_{r^2\to 0}\frac{\sin(r^2)\cdot 2r}{4r^3}=\frac{1}{2}\cdot \lim_{r^2\to 0}\frac{\sin(r^2)}{r^2}=\frac{1}{2}\cdot 1=\frac{1}{2}\).