Zeigen Sie, dass f überall zweimal partiell differenzierbar ist, dass aber D1 D2 f(0) \neq D2 D1f(0) .

Question

Aufgabe:

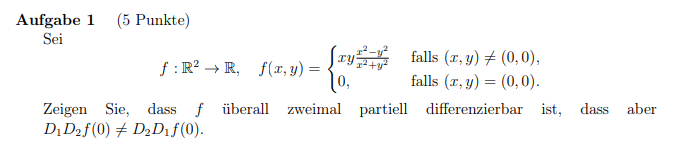
Text erkannt:

Aufgabe 1
Sei
(5 Punkte)
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll} x y \frac{x^{2}-y^{2}}{x^{2}+y^{2}} & \text { falls }(x, y) \neq(0,0), \\ 0, & \text { falls }(x, y)=(0,0) . \end{array}\right. \)
Zeigen Sie, dass \( f \) überall zweimal partiell differenzierbar ist, dass aber \( D_{1} D_{2} f(0) \neq D_{2} D_{1} f(0) \).

Comments

Außerhalb des Nullpunkts wird f durch eine differenzierbare Verknüpfung von Polynomen - also beliebig oft differenzierbaren Funktion - dargestellt, ist also beliebig oft stetig differenzierbar.

Im Nullpunkt musst Du mit der Definition der parteillen Ableitung durch Differenzenquotienten arbeiten. Für die gemischten Ableitungen brauchst Du D_1 f(x,y)  und D_2 f(x,y)  für punkte \((x,y) \neq (0,0)\)- die kannst Du doch mal nach den einschlägigen Regeln berechnen