Zeigen Sie, dass das Taylor-Polynom bei x0 die gleichen Ableitungen wie die zugrunde liegende Funktion hat, also …

Question

Hallo, könnte mir jemand helfen, dieses Problem zu lösen? Zeigen Sie, dass das Taylor-Polynom bei x0 die gleichen Ableitungen wie die zugrunde liegende Funktion hat, also dass für 0≤k≤N gilt

Ich habe versucht einfach die Ableitung zu bilden jedoch sind meine Ergebnisse falsch

Ich bedanke mich im Voraus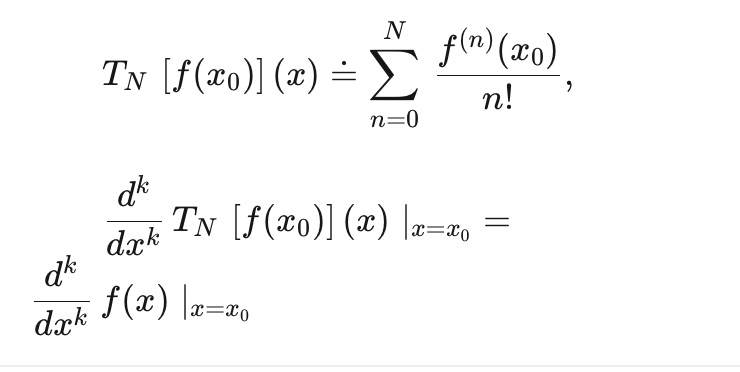

Text erkannt:

\( \begin{array}{c}T_{N}\left[f\left(x_{0}\right)\right](x) \doteq \sum \limits_{n=0}^{N} \frac{f^{(n)}\left(x_{0}\right)}{n !}, \\ \left.\frac{d^{k}}{d x^{k}} T_{N}\left[f\left(x_{0}\right)\right](x)\right|_{x=x_{0}}= \\ \left.\frac{d^{k}}{d x^{k}} f(x)\right|_{x=x_{0}}\end{array} \)

Comments

Zunächst fehlt bei dem Taylorpolynom noch ein Term - (x-x_0)^n.

Dann kannst Du doch einfach das Polynom einmal, zweimal differenzieren .....

Answer 1

Hallo wenn du T das bei dir nur eine Zahl ist mit (x-x0)^n ergänzt,  und k mal ableitest, verschwinden alle Ableitungen bis zu k-2 ten, bei der k-1 ten steht (x-x0)^0  alle anderen haben Faktoren mit x-x0 sind also 0 bei x0

also ist es einfach. sonst rechne mal die z.b. dritte oder 4 t3 Ableitung aus um zu sehen wie es läuft.

lul