Transformation einer Funktion / Jacobimatrix

Question

Aufgabe:

Wie Berechne ich g(z)?

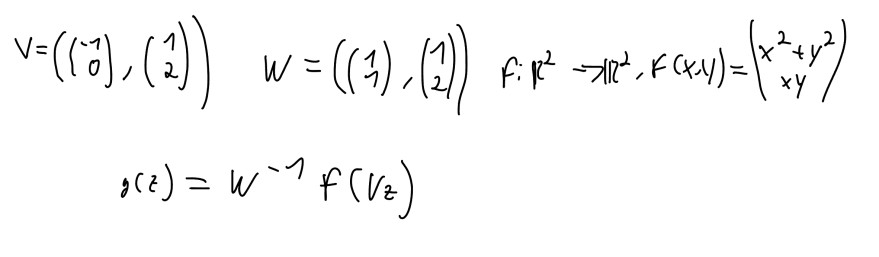
Text erkannt:

\( \begin{array}{c}V=\left(\left(\begin{array}{c}1 \\ 0\end{array}\right),\left(\begin{array}{l}1 \\ 2\end{array}\right)\right) \quad W=\left(\left(\begin{array}{l}1 \\ 1\end{array}\right),\left(\begin{array}{l}1 \\ 2\end{array}\right)\right) \quad f ; R^{2}-7 \mathbb{R}^{2}, f(x, y)=\left(\begin{array}{c}x^{2}+y^{2} \\ x y\end{array}\right) \\ g(z)=W^{-1} f\left(V_{z}\right)\end{array} \)

Problem/Ansatz:

Die Inverse von W zu bestimmen ist kein Problem, allerdings bin ich bei f(Vz) etwas ratlos. Muss ich da einfach den Vektor der Funktion mit der Matrix V multiplizieren? Bin in dieser Hinsicht etwas verwirrt, da ich im Anschluss die Jacobimatrix von g(z) bestimmen soll.

Comments

Hallo

keine Ahnung was hier z bedeuten soll, ist das genau die Originalaufgabe, dann sind vielleicht die 2 möglichen z die Vektoren aus V? also einmal x=1,y=0 einmal x=1, y=2 in f einsetzen?

Aber das ist nur ne Vermutung. kannst du die exakte Originalaufgabe posten?

lul

---

Genau das frage ich mich auch

Die Aufgaben Stellung ist erstmal g(z) zu bestimmen (wie oben beschreiben) und dann davon die Jacobimatrix zu berechnen.

---

Ich versteh jetzt, was du meinst. Z ist kein Index von V. Es steht explizit V*z

---

Originalaufgabe: https://appurl.io/sPc5aftjLG

---

Hallo

mir war nicht klar, dass V ne Matrix sein soll, ich dacht der Span der 2 Vektoren . dann ist V*z eben V*\( \begin{pmatrix} z_1\\z_2\\z_3 \end{pmatrix} \)

Gruß lul

---

Danke, aber bekomme ich dann für g(z) nicht auch eine 2x2 Matrix raus? Eine Jacobimatrix kann man doch nur von einem Spaltenvektor berechnen oder sehe ich da was falsch?

---

Ich sehe da:

$$Vz=\begin{pmatrix} -1 & 1 \\ 0 & 2\end{pmatrix}\begin{pmatrix} z_1\\ z_2 \end{pmatrix}=\begin{pmatrix} z_2-z_1 \\ z_2 \end{pmatrix}$$

$$f(Vz)=\begin{pmatrix} (z_2-z_1)^2+z_2^2 \\ (z_2-z_1)z_2 \end{pmatrix}$$

$$W^{-1}f(Vz)=\begin{pmatrix}2 & -1 \\ -1 & 1\end{pmatrix}\begin{pmatrix} (z_2-z_1)^2+z_2^2 \\ (z_2-z_1)z_2 \end{pmatrix}$$