Bei a habe ich schon die notwendige Bedingung gemacht mit der pq Formel und dann kam T1=2k-2 heraus und t2= 2
Wie und was muss ich jetzt bei der Hinreichende Bedingungen machen?
Und was muss ich bei b machen?
Und bei c habe ich für t einmal 0 und einmal 4 herausbekommen, ist das richtig?
Und bei d muss ich da einmal k einsetzen für 3 und 5 und einmal t mit 0 und 4 oder was muss ich da tun?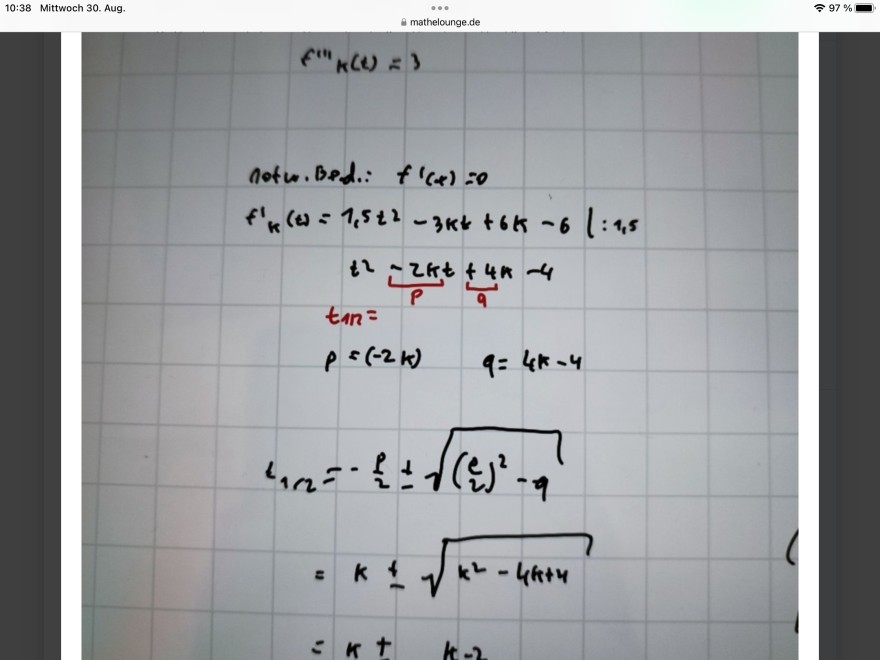
Text erkannt:
10:38 Mittwoch 30. Aug.
mathelounge.de
\( f^{\prime \prime \prime} k(t)=3 \)
notur.Bed.: \( f^{\prime}(x)=0 \)
\( \begin{aligned} f_{k}^{\prime}(t) & =1,5 t^{2}-3 k t+6 k-6 \quad \mid: 1,5 \\ t^{2} & =\frac{2 k t}{p}+\frac{4 k-4}{9}= \\ p & =(-2 k) \quad q=4 k-4 \\ l_{1 / 2} & =-\frac{p}{2} \pm \sqrt{\left(\frac{l}{2}\right)^{2}-q} \\ & =k \pm \sqrt{k^{2}-4 k+4} \\ & =k \pm \sqrt{k-2} \end{aligned} \)
Upload failed: [object Object]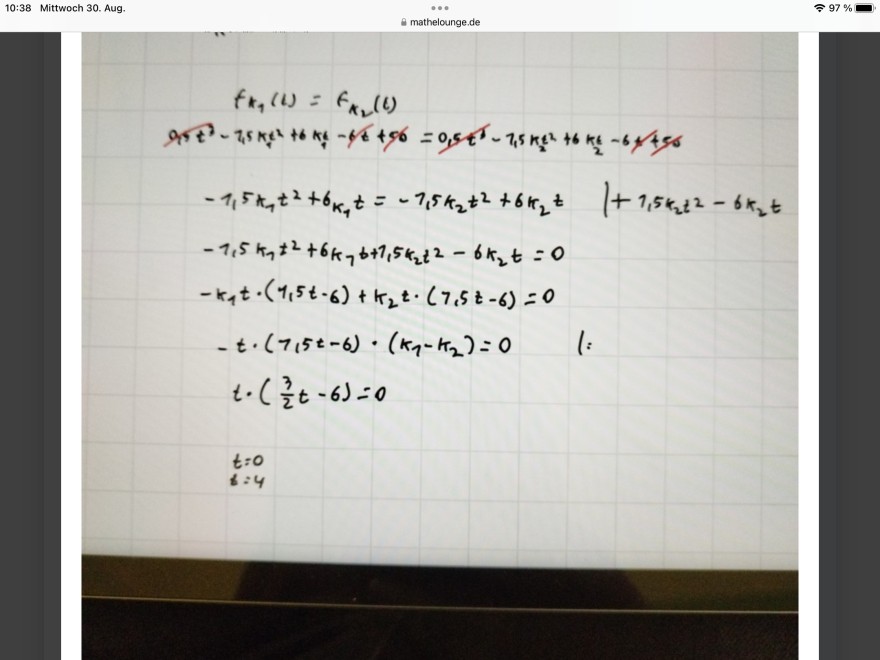
Text erkannt:
10:38 Mittwoch 30. Aug.
a mathelounge.de
\( \begin{array}{l} f_{k_{1}}(t)=f_{k_{2}}(l) \\ 9 t^{2}-1,5 k_{1}^{2}+6 k_{1}-6 t+96=0,5 t^{6}-1,5 k_{2} t^{2}+6 k_{2}-6,456 \\ -1,5 k_{1} t^{2}+6 k_{1} t=-1,5 k_{2} t^{2}+6 k_{2} t \quad \mid+1,5 k_{2} t^{2}-6 k_{2} t \\ -1,5 k_{1} t^{2}+6 k_{1} t+1,5 k_{2} t^{2}-6 k_{2} t=0 \\ -k_{1} t \cdot(1,5 t-6)+k_{2} t \cdot(7,5 t-6)=0 \\ -t \cdot(1,5 t-6) \cdot\left(k_{1}-k_{2}\right)=0 \quad \mid: \\ t \cdot\left(\frac{3}{2} t-6\right)=0 \\ t=0 \\ t=4 \end{array} \)