Hallo
da das wohl in der Schule benutzt werden soll führen bei Herleitungen nicht zu einfachen Formeln für das Trapez, wie finden SuS dein G'? wennschon sollte die Oberseite G' sin und dann ist die Fläche nicht A=2*g*h/2
deine erste Herleitung gilt ja nur für ein spezielles Trapez, und auch dpa müsstest du g noch ersetzen ? im Prinzip kann man natürlich 2 Dreiecke abschneiden, muss aber dann auf die eigentliche Trapezformel kommen indem man die 2 Dreiecke zusammen berechnet.
die übliche Figur ist für 2A . oder du drehst die 2 Dreiecke um und errechnet ihre doppelte Fläche 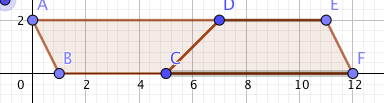
Gruß lul