Aufgabe:
Kontrollaufgabe: Von A= Düsseldorf, phi = 51.2°, lamda = 6.8° nach B = San Francisco phi = 37.8°, lamda = -122.4° (122.4° W). Bestimmen Sie die Koordinaten des nördlichsten Punktes F.
Problem/Ansatz:
phi von F soll 67.1° N sein, aber ich bekomme 56.83° N
Text erkannt:
Anwendungen der Mathematik: 5. Klasse
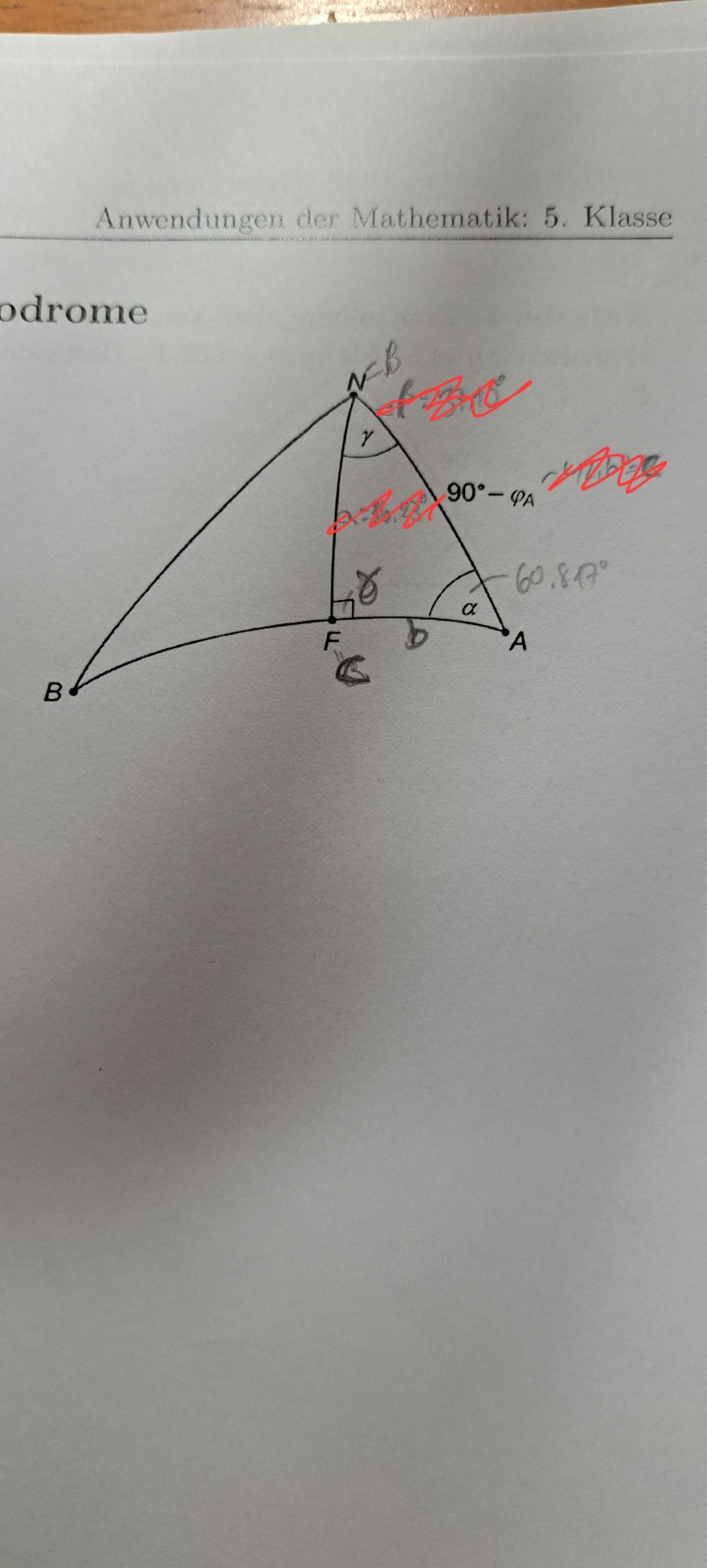
odrome
alpha gleich 60.817° ist in der Aufgabe schon gegeben
Text erkannt:
Anwendungen der Mathematik: 5. Klasse
odrome
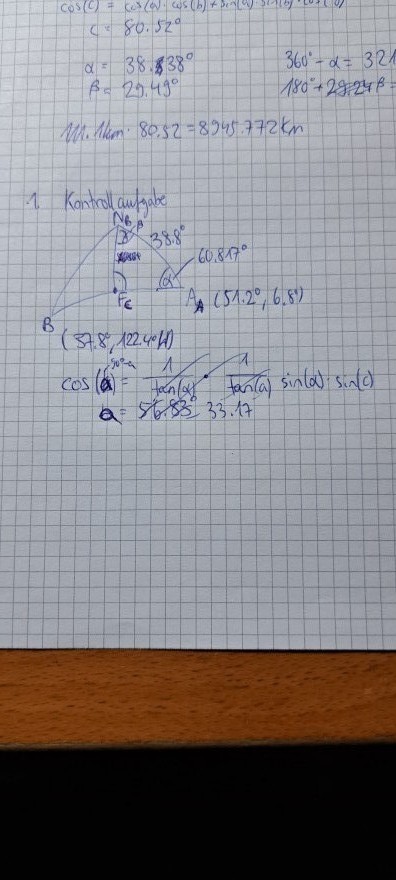
Text erkannt:
\( \begin{array}{ll} c=80.52^{\circ} & 360^{\circ}-\alpha=321 \\ \alpha=38.38^{\circ} & 180^{\circ}+29.24 \beta= \\ \beta=29.49^{\circ} & \\ \text { Wh. } 1 \mathrm{~km} \cdot 80.52=8945.772 \mathrm{~km} \end{array} \)
1 Kontroll autgabe