Wie groß muß die unter einem Winkel von 35° zum Boden wirkende Kraft F sein?

Question

Aufgabe:

Ein Körper der Masse m = 400 kg soll auf der Unterlage verschoben werden und benötigt dazu eine horizontale Kraft von 600 N.
Wie groß muß die unter einem Winkel von 35° zum Boden wirkende Kraft F sein?
Lösen Sie die Aufgabe zeichnerisch und rechnerisch.

Problem/Ansatz:

In der Musterlösung wird mit der Formel:

cos(35)= Fsoll/F gerechnet

wie kommt man aber auf diese Formel?

Also ich bräuchte eine Erklärung wie man auf die Formel kommt ?

DANKE

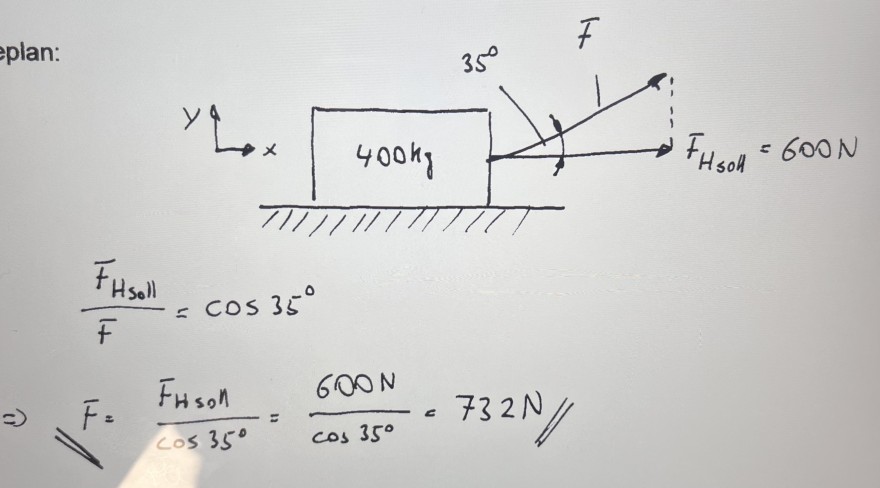
Text erkannt:

\( \begin{aligned} & \frac{F_{H_{s_{0} I}}}{F}=\cos 35^{\circ} \\ \Rightarrow & F=\frac{F_{H \operatorname{son}}}{\cos 35^{\circ}}=\frac{600 \mathrm{~N}}{\cos 35^{\circ}}=732 \mathrm{~N}\end{aligned} \)

Comments

Von der schräg ansetzenden Kraft F wirkt nur die horizontale Komponente (parallel zum Boden) der Fortbewegung des schweren Körpers. Die vertikale Komponente der Zugkraft (senkrecht zum Boden) bleibt praktisch wirkungslos. Insbesondere ist sie deutlich zu klein, um etwa den Block vom Boden abzuheben.

Den rechnerischen Teil (mit dem Cosinus) haben andere schon erklärt.

Answer 1

die Kräfte ergeben ein rechtwinkliges Dreieck mit den Werten F, F_Hsoll und α. F ist die Hypotenuse F_Hsoll die Ankathete.

Answer 2

Dieser Ansatz ergibt sich aus der Definition des Kosinus.