basis von vektorspan und einheitsvektoren

Question

Aufgabe:Basis von Span bestimmen und Einheitsvektor. wie kann ich die aufgaben lösen ?

Problem/Ansatz:

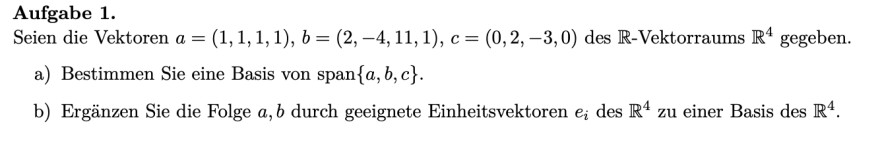
Text erkannt:

Aufgabe 1.
Seien die Vektoren \( a=(1,1,1,1), b=(2,-4,11,1), c=(0,2,-3,0) \) des \( \mathbb{R} \)-Vektorraums \( \mathbb{R}^{4} \) gegeben.
a) Bestimmen Sie eine Basis von \( \operatorname{span}\{a, b, c\} \).
b) Ergänzen Sie die Folge \( a, b \) durch geeignete Einheitsvektoren \( e_{i} \) des \( \mathbb{R}^{4} \) zu einer Basis des \( \mathbb{R}^{4} \).

Answer 1

a) \( a, b, c \) sind linear unabhängig, bilden also eine Basis.

b) Bilde b-a und b-2a , dann siehst du, dass man e₂ und e₃ 

nehmen kann.

Comments

bei der a) soll ich ja eine Basis bilden. wie geht das ?

---

Eine Basis ist ein lin. unabhängiges Erzeugendensystem.

Das sind a,b,c.