Aufgabe:
Hallo, kann jemand erläutern was die markierten Begriffe bedeuten. Siehe Bild.
Es wurde ja nichts "eingesetzt", was iwie verwirrend ist. Und sonst konnte ich zu diesem Begriff auch bisher nichts finden.
Problem/Ansatz:

Text erkannt:
2. Aufgabe: \( k \)-Formen
Seien \( v=(1,-3,0)^{T} \) und \( w=(2,2,-1)^{T} \), und \( \alpha, \beta \) die durch \( \alpha=d x+3 d y-d z, \beta=-d x+ \) \( 2 d y+d z \) gegebenen 1-Formen auf \( \mathbb{R}^{3} \). Bestimmen Sie \( \alpha(v), \alpha(w), \beta(v), \beta(w), \alpha \wedge \beta, \alpha \wedge \beta(v, w) \) und \( \alpha \wedge \beta \wedge d z \).
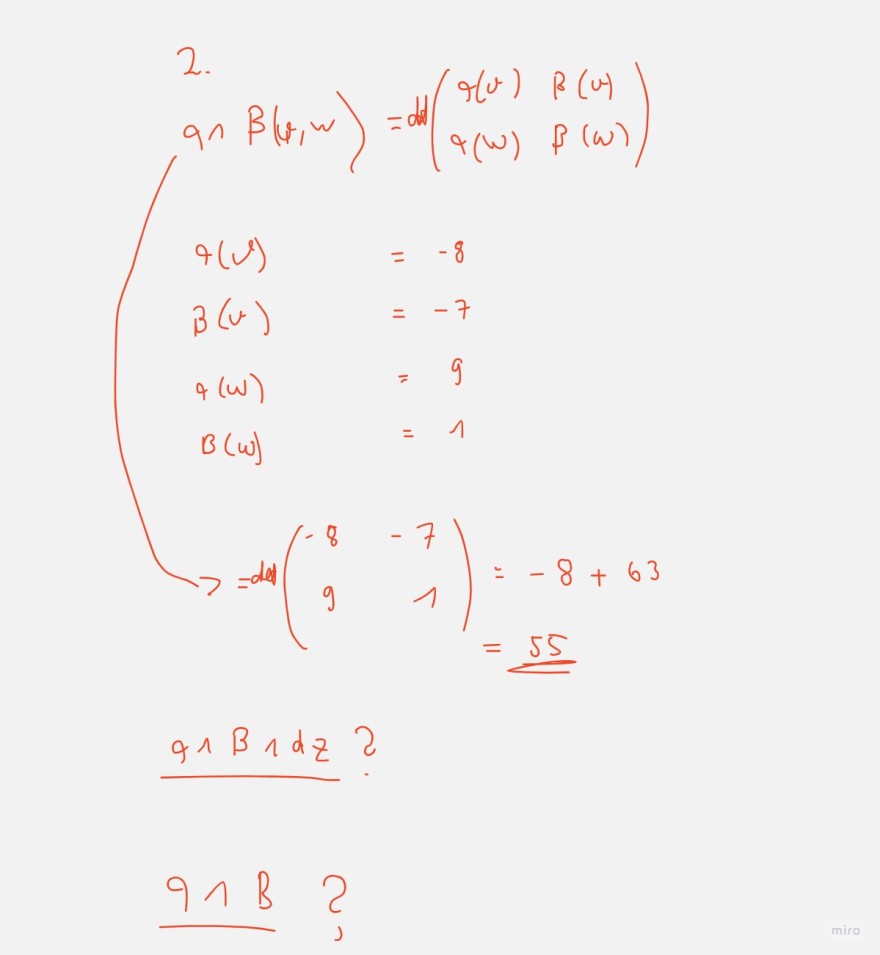
Text erkannt:
2.
\( \begin{array}{l} q \wedge \beta(\psi, \omega)=d d\left(\begin{array}{ll} q(v) & \beta(v) \\ q(\omega) & \beta(\omega) \end{array}\right) \\ q(v)=-8 \\ \beta(v)=-7 \\ q(\omega)=9 \\ B(\omega)=1 \\ =\operatorname{ded}\left(\begin{array}{rr} -8 & -7 \\ 9 & 1 \end{array}\right)=-8+63 \\ =55 \\ \end{array} \)
\( q \wedge \beta \wedge d z \) ?