Beweis Integrationsgrenzen, Doppelintegral

Question

Hey, ich habe diese Aufgabe in einem der Vorbereitungsblätter für meine Ana2 Prüfung gefunden, für die es noch keine Lösungesfolien gibt. Bei der komme ich gerade auf keinen richtigen Ansatz. Hätte da einer eine Idee?

Zu zeigen: Wenn \( a<b \) ist, dann gilt:
\( \int \limits_{a}^{b} \int \limits_{a}^{x} f(x, y) d y d x=\int \limits_{a}^{b} \int \limits_{y}^{b} f(x, y) d x d y \)

Comments

So wie sie dasteht ist die Aussage falsch. Betrachte als Gegenbeispiel die Funktion f mit
f(x,y) = 0 falls x rational, f(x,y) = sin(2π/(x-a)*(y-a)) falls x irrational.

---

für f(x,y) = 0 kommt doch aber auf beiden Seiten 0 heraus..?

---

auf beiden Seiten 0 heraus

Nein.
Die beiden Definitionen sind zusammen zu lesen. Die erste ist für rationale, die zweite für irrationale x-Werte anzuwenden.

Wahrscheinlich (hoffentlich) verbietet der vollständige Aufgabentext derartige Konstruktionen.

---

 

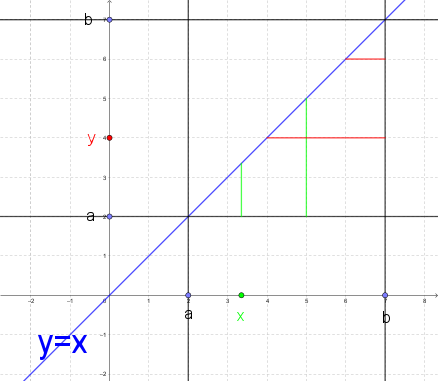
Man betrachte auf der linken Seite zunächst das innere Integral.
Für einen festen x-Wert wird das Integral in y-Richtung von a bis zur blauen Winkelhalbierenden y=x berechnet. (grün). Anschließend werden all diese Werte der grünen Streifen von x=a bis x=b in x-Richtung integriert, das ganze (untere) Dreieck ist somit spaltenweise abgescannt.

Auf der rechten Seite gibt das innere Integral für festes y zunächst den Wert längs einer Zeile von links (x=y) bis rechts (x=b) an (rot), anschließend werden all diese Zeilenwerte von unten (y=a) bis oben (y=b) aufintegriert.

Und wenn man Glück hat, kommt bei beiden Methoden dasselbe heraus.

---

Meintest du f(x,y)=sin(2π/((x-a)*(y-a))) also, dass (x-a)(y-a) beides im Nenner steht oder nur (x-a) und dann wird an den Bruch (y-a) multipliziert?

---

Aufgabe hat da nichts ausgeschlossen. Habe es jetzt mal so gemacht, bin mir jetzt aber auch nicht 100% sicher…

---

Meintest du f(x,y)=sin(2π/((x-a)*(y-a)))

Ich meinte das, was ich geschrieben habe.

---

Gut, wollte nur fragen. Habe im Endeffekt garkein Gegenbeispiel gebraucht sollte mein Ansatz so stimmen. (Habe den Satz von Fubini benutzt)

---

Habe den Satz von Fubini benutzt

Nein, das hast du nicht.
Der Satz von Fubini macht eine Aussag über Integrale, aber deine Ausführungen kreisen lediglich darum, einen Nachweis für B1 = B2 zu führen.
Um den Satz von Fubini benutzen zu können, muss man überdies zunächst prüfen, ob die Voraussetzungen, unter denen seine Folgerung gilt, überhaupt erfüllt sind. Davon steht bei dir kein Wort.

---

Ich habe den Satz von Fubini in der Hinsicht benutzt, dass ich die Differentiale dx und dx vertauscht habe. Der Rest hat natürlich mit Fubini nichts zu tun. Fubinis Satz muss ich nicht nachweisen, da der in unserem Skript schon behandelt wurde. Wenn du mir helfen willst, gerne, aber warum so passiv aggressiv??

---

Mein Gedanke war eben, dass ich nach Fubini die Differentiale vertauschen darf, und dann eben nurnoch nachweisen muss dass die Bereiche gleich sind damit die Gleichung vollständig gilt.

---

Jawollski✅..