Lösen von Wurzel- und Exponentialgleichungen

Question

Kann mir jemand helfen beim lösen dieser Aufgaben?

c) \( \sqrt{8-2 a}=\sqrt{5-a}-1 \)

d) \( 3 \cdot 25^{x}=-5+8 \cdot 5^{x} \)

e) \( 3^{4 y+1}+81^{y+1}=9^{2 y-1} \)

Comments

Du schreibst "quadratische-gleichungen".

Es sind keine quadratischen Gleichungen.

Ich habe den Titel angepasst. "Lößen von komplizierten aufgaben" war nämlich auch nicht wirklich aussagekräftig.

---

danke, das ist sehr nett

Answer 1

Hallo,

Aufgabe a)

Quadriere beide Seiten der Gleichung:

\(\sqrt{8-2a}=\sqrt{5-a}-1\\ 8-2a=5-a-2\sqrt{5-a}+1\\\)

Sortiere und quadriere wieder:

\(2-a=-2\sqrt{5-a}\\ 4-4a+a^2=4\cdot(5-a)\\\)

Den Rest der Aufgabe schaffst du sicher selber. Vergiss die Probe nicht, denn Quadrieren ist keine Äquivalenzumformung.

Gruß, Silvia

Answer 2

d) 3*5^(2x)- 8*5^x+5 = 0

5^x = z

3z^2-8z+5 = 0

abc- Formel:

z1/2= (8+-√(64-4*3*5))/(2*3) = (8+-2)/6

z1= 1

z2= 5/3

5^x= 1

x1= ln1/ln5 = 0 -ln5 = -ln5

5^x= 5/3

x2= ln(5/3)/ln5 = (ln5-ln3)/ln5 = 1 - ln3/ln5

e) 3^(4y+1)+ 3^(4y+4)- 3^(4y-2) =0

3*3^(4y)+3^4*3^(4y)-3^(4y)/3^2 = 0

84*3^(4y)-3^(4y)/9 = 0

756*3^(4y)- 3^(4y) = 0

755*3^(4y)= 0

3^(4y) =0

Keine Lösung.

Answer 3

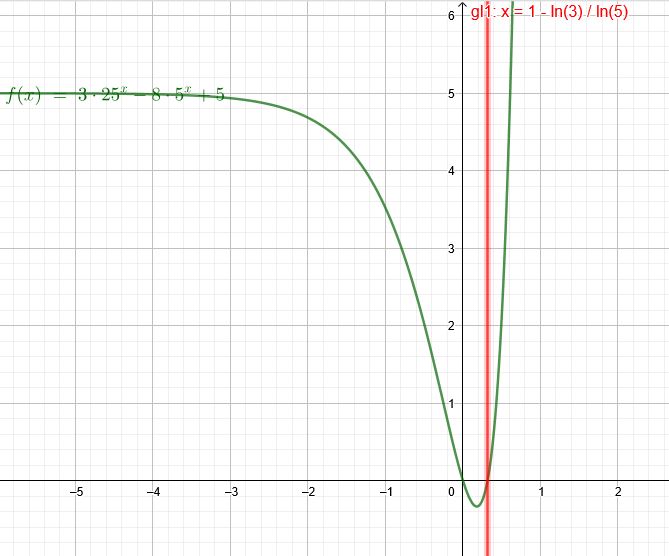
\( 3 \cdot 25^{x}=-5+8 \cdot 5^{x} \)

Berechnung ohne Substitution:

\( 3 \cdot 25^{x}-8 \cdot 5^{x}=-5 \)

\( 25^{x}-\frac{8}{3} \cdot 5^{x}=-\frac{5}{3} \)

\( 5^{2x}-\frac{8}{3} \cdot 5^{x}+(\frac{4}{3})^2=-\frac{5}{3}+(\frac{4}{3})^2=-\frac{15}{9}+\frac{16}{9}=\frac{1}{9} \)

\( (5^{x}-\frac{4}{3} )^2=\frac{1}{9}    |\pm\sqrt{~~}\)

1.)

\( 5^{x}-\frac{4}{3} =\frac{1}{3}  \)

\( 5^{x} =\frac{5}{3}  \)

\( x\cdot ln(5)  =ln(5)- ln(3)\)

\( x_1 =1- \frac{ln(3)}{ln(5)}\)

2.)

\( 5^{x}-\frac{4}{3} =-\frac{1}{3}  \)

\( 5^{x} =1  \)

\(x_2 =0  \)

Comments

Die quadratische Ergänzung dankt dir und wird dir ein Denkmal setzen lassen in der aula salvatorum omnium in oblivionem incisurorum. :)

Answer 4

3·25^x = -5 + 8·5^x

3·(5^x)^2 = -5 + 8·5^x

3·(5^x)^2 - 8·5^x + 5 = 0

Subst. 5^x = z

3·z^2 - 8·z + 5 = 0 --> z = 5/3 ∨ z = 1

Resubst.

5^x = 5/3 --> x = 1 - LN(3)/LN(5) = 0.3174

5^x = 1 --> x = 0