Kreuzprodukt mit Parameter und Sinuswinkel

Question

Aufgabe:

Es seien

$v:=\left(\begin{array}{l} 1 \\ \alpha \\ 2 \end{array}\right), w:=\left(\begin{array}{l} 4 \\ 0 \\ 3 \end{array}\right) \in \mathbb{R}^{3}$

für ein $\alpha \in \mathbb{R}$. Bestimmen Sie das Kreuzprodukt $v \times w$ in Abhängigkeit von $\alpha$. Wie muss $\alpha$ gewählt werden damit $\sin \angle(v, w)=\sqrt{\frac{1}{3}}$ gilt.

Problem/Ansatz:

Hallo, bei folgender Aufgabe, weiß ich leider nicht wie ich vorgehen kann. Kreuzprodukt bilden ist kein Problem, aber ich komme nicht darauf wie man den Sinuswinkel hier bestimmen kann.

LG

Answer 1

Wegen

        $\sin^2\angle(v,w) = 1-\cos^2\angle(v,w)$

und

        $\cos\angle(v,w) = \frac{v*w}{|v|\cdot |w|}$

genügt es, die Gleichung

      $\frac{1}{3} = 1-\left(\frac{v*w}{|v|\cdot |w|}\right)^2$

zu lösen.

Comments

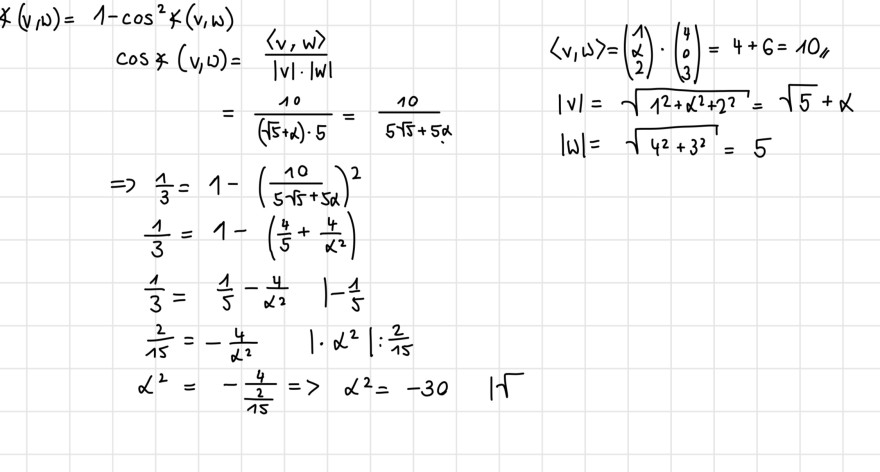
Text erkannt:

$\begin{array}{l}x(v, \omega)=1-\cos ^{2} k(v, \omega) \\ \cos x(v, v)=\frac{\langle v, w\rangle}{|v| \cdot|w|} \\ \langle v, \omega\rangle=\left(\begin{array}{l}1 \\ \alpha \\ 2\end{array}\right) \cdot\left(\begin{array}{l}4 \\ 0 \\ 3\end{array}\right)=4+6=10 / 1 \\ =\frac{10}{(\sqrt{5}+\alpha) \cdot 5}=\frac{10}{5 \sqrt{5}+5 \alpha} \\ |v|=\sqrt{1^{2}+\alpha^{2}+2^{2}}=\sqrt{5}+\alpha \\ |\omega|=\sqrt{4^{2}+3^{2}}=5 \\ \Rightarrow \frac{1}{3}=1-\left(\frac{10}{5 \sqrt{5}+5 \alpha}\right)^{2} \\ \frac{1}{3}=1-\left(\frac{4}{5}+\frac{4}{\alpha^{2}}\right) \\ \left.\frac{1}{3}=\frac{1}{5}-\frac{4}{\alpha^{2}} \right\rvert\,-\frac{1}{5} \\ \frac{2}{15}=-\frac{4}{\alpha^{2}} \quad\left|\cdot \alpha^{2}\right|: \frac{2}{15} \\ \left.\alpha^{2}=-\frac{4}{\frac{2}{15}} \Rightarrow \alpha^{2}=-30 \quad \right\rvert\, \gamma \\\end{array}$

Text erkannt:

10:15 Montag 15. Jan.
$\begin{array}{l} \chi(v, \omega)=1-\cos ^{2} K(v, \omega) \\ \cos x(v, v)=\frac{\langle v, w\rangle}{|v| \cdot|w|} \\ \langle v, \omega\rangle=\left(\begin{array}{l} 1 \\ \alpha \\ 2 \end{array}\right) \cdot\left(\begin{array}{l} 4 \\ 0 \\ 3 \end{array}\right)=4+6=10 / 11 \\ =\frac{10}{(\sqrt{5}+\alpha) \cdot 5}=\frac{10}{5 \sqrt{5}+5 \alpha} \\ |v|=\sqrt{1^{2}+\alpha^{2}+2^{2}}=\sqrt{5}+\alpha \\ |\omega|=\sqrt{4^{2}+3^{2}}=5 \\ \Rightarrow \frac{1}{3}=1-\left(\frac{10}{5 \sqrt{5}+5 \alpha}\right)^{2} \\ \frac{1}{3}=1-\left(\frac{4}{5}+\frac{4}{\alpha^{2}}\right) \\ \left.\frac{1}{3}=\frac{1}{5}-\frac{4}{\alpha^{2}} \right\rvert\,-\frac{1}{5} \\ \frac{2}{15}=-\frac{4}{\alpha^{2}} \quad\left|\cdot \alpha^{2}\right|: \frac{2}{15} \\ \left.\alpha^{2}=-\frac{4}{\frac{2}{15}} \Rightarrow \alpha^{2}=-30 \quad \right\rvert\, \sqrt{ } \\ \end{array}$

Danke für die Antwort.

Nur kann ich bei meiner Rechnung nicht die Wurzel ziehen. Habe ich etwa falsch gerechnet?

---

Warum um Himmels Willen machst du nach dem hier (falls es stimmt)

mit

$\frac{2}{3}=\left(\frac{10}{5 \sqrt{5}+5 \alpha}\right)^{2}$ weiter?

Answer 2

Nutze doch viel lieber $|v\times w| = |v||w|\sin\angle(v,w)$. Denn das Kreuzprodukt hast du ja nicht umsonst berechnet.