Aufgabe:

Text erkannt:
13.1 Sei \( V \) ein \( \mathbb{K} \)-Vektorraum mit \( \operatorname{dim}(V)=7 \) und \( U, W \leq V \). Beweisen oder widerlegen Sie:
a) Falls \( \operatorname{dim}(U)+\operatorname{dim}(W)>7 \), so gilt \( \operatorname{dim}(U \cap W)>1 \)
b) Wenn \( U+W=V \), so ist \( \operatorname{dim}(U)+\operatorname{dim}(W)=7 \)
c) Wenn \( \operatorname{dim}(U+W)=7 \), so ist \( U+W=V \)
d) Sei \( \operatorname{dim}(U)=2 \) und \( \operatorname{dim}(W)=4 \), so ist \( 2 \leq \operatorname{dim}(U+W) \leq 6 \)
e) Es existieren \( U, W \) mit \( \operatorname{dim}(U)=2 \) und \( \operatorname{dim}(W)=4 \), so dass \( \operatorname{dim}(U+W)=5 \)
f) Es existieren \( U, W \) mit \( \operatorname{dim}(U)=2 \) und \( \operatorname{dim}(W)=4 \), so dass \( \operatorname{dim}(U+W)=3 \) \( (1+1+1+1+1+1 \) Punkte \( ) \)
Problem/Ansatz:
Bei A bin ich mir noch sehr unschlüssig ob es wahr oder falsch ist. Ich bin mir sicher , dass die Summe auf alle Fälle größer als 7 sein kann aber ob der Schnitt dann größer als 1 ist bin ich mir nicht sicher bzw weiß nicht wie ich es zeigen kann, wenn es so ist. Kann man mir dabei helfen ?
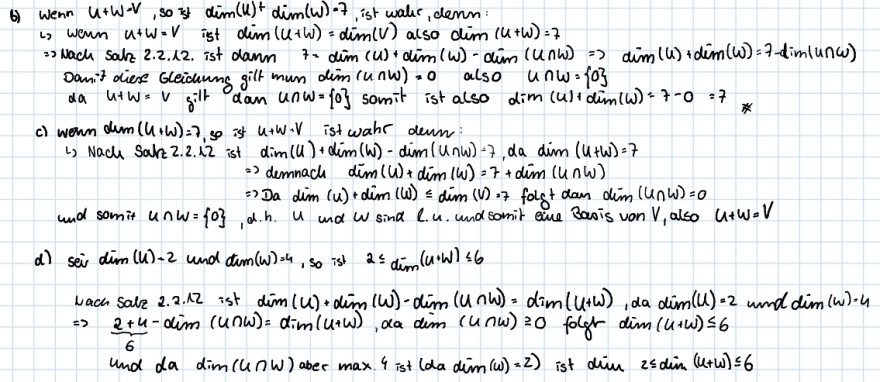
Text erkannt:
b) Wenn \( u+w=v \), so ks \( \operatorname{dim}(u)^{+} \operatorname{dim}(w)=7 \), ist wahe, denn:
() \( w \) enn \( u+w=v \) ist \( \operatorname{dim}(u+w)=\operatorname{dim}(v) \) also \( \operatorname{dim}(u+w)=7 \)
\( \Rightarrow \) Nach Salz 2.2.12. ist dann \( 7=\operatorname{dim}(u)+\operatorname{dim}(\omega)-\operatorname{dim}(u \cap \omega) \Rightarrow \operatorname{dim}(u)+\operatorname{dim}(\omega)=7-\operatorname{dim}(u \cap \omega) \)
Danit dies Gceichung gilt mun \( \operatorname{dim}(u \cap w)=0 \) also \( u \cap w=\{0\} \)
da \( u+w=v \) gitt dan \( u \cap w=\{0\} \) somit ist also \( \operatorname{dim}(u)+\operatorname{dim}(\omega)=7-0=7 \)
c) wenn \( \operatorname{dum}(u+w)=7,95 \) is \( u+w \cdot v \) ist wahe deun:
(5) Nacle Salz 2.2. i2 ist \( \operatorname{dim}(u)+\operatorname{dim}(w)-\operatorname{dim}(u \cap w)-7, d a \operatorname{dim}(u+w)=7 \)
\( \Rightarrow \) demnach \( \operatorname{dim}(u)+\operatorname{dim}(\omega)=7+\operatorname{dim}(u \cap \omega) \)
\( \Rightarrow \) Da \( \operatorname{dim}(u)+\operatorname{dim}(w) \leq \operatorname{dim}(v)=7 \) folgt dan \( \operatorname{dim}(u \cap w)=0 \)
und somit \( u \cap w=\{0\} \), d.h. \( u \) und \( w \sin \alpha \) C.u. und somit eive Basis von \( V \), also \( u+w=V \)
d) \( \operatorname{sei} \operatorname{dim}(u)=2 \) und \( \operatorname{dum}(\omega)=4 \), so ist \( 2 \leq \operatorname{dim}(u+w) \leq 6 \)
wach salz 2.2.12 ist \( \operatorname{dim}(u)+\operatorname{dim}(\omega)-\operatorname{dim}(u \cap \omega)=\operatorname{dim}(u+\omega), \operatorname{da} \operatorname{dim}(u)=2 \) und \( \operatorname{dim}(\omega)=4 \) \( \Rightarrow \quad \frac{2+u}{6}-\operatorname{dim}(u \cap \omega)=\operatorname{dim}(u+\omega), \operatorname{dadim}(u \cap \omega) \geq 0 \) folgr \( \operatorname{dim}(u+w) \leq 6 \)
und da \( \operatorname{dim}(u \cap w) \) aber \( \max 4 \) ist \( (d a \operatorname{dim}(w)=2) \) ist \( \operatorname{dim} 2 \leq \operatorname{dim}(u+w) \leq 6 \)
Für b, c und d habe ich entschieden, dass es wahr ist und dies wie auf dem Bild bewiesen, ist das aber so richtig?
Und für e bin ich der Meinung es ist wahr und für f denke ich ist es falsch aber hier habe ich auch nicht wirklich eine Idee, wie ich es erklären kann. Kann mir hier auch noch jemand helfen?