Lineare Unabhängigkeit in F5

Question

Aufgabe:

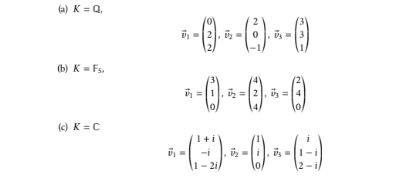
Text erkannt:

(a) \( K=\mathrm{Q} \),
\( \vec{v}_{1}=\left(\begin{array}{l} 0 \\ 2 \\ 2 \end{array}\right), \vec{v}_{2}=\left(\begin{array}{c} 2 \\ 0 \\ -1 \end{array}\right), \vec{v}_{3}=\left(\begin{array}{l} 3 \\ 3 \\ 1 \end{array}\right) \)
(b) \( K=\mathrm{F}_{5} \),
\( \vec{v}_{1}=\left(\begin{array}{l} 3 \\ 1 \\ 0 \end{array}\right), \vec{v}_{2}=\left(\begin{array}{l} 4 \\ 2 \\ 4 \end{array}\right), \vec{v}_{3}=\left(\begin{array}{l} 2 \\ 4 \\ 0 \end{array}\right) \)
(c) \( K=\mathrm{C} \)
\( \vec{v}_{1}=\left(\begin{array}{c} 1+i \\ -i \\ 1-2 i \end{array}\right), \vec{v}_{2}=\left(\begin{array}{l} 1 \\ i \\ 0 \end{array}\right), \vec{v}_{3}=\left(\begin{array}{c} i \\ 1-i \\ 2-i \end{array}\right) \)

Problem/Ansatz:

a) und c) kann ich lösen, aber bei b) habe ich Probleme vorzugehen. Ich verstehe nicht, wie man in F5 genau operiert. Könnte mir bitte jemand helfen?

Answer 1

In \(\mathbb{F}_5\) musst du lediglich immer modulo 5 rechnen.

Comments

Ich denke, dass ich Modulo 5 rechnen kann, aber ich habe trotzdem Probleme beim Vorgehen. In meinen Büchern finde ich nichts, und das Skript ist unvollständig.

---

Wie zeigst du denn die Unabhängigkeit in den anderen Körpern?

---

Das ist mir schon klar.

---

Dann mach das doch hier auch. Die Zeilenstufenform bspw. bekommst du auf dieselbe Weise wie in anderen Körpern. Beachte halt das Rechnen von modulo 5 in den Zwischenschritten.

---

Ich denke, dass ich modulo Rechnen nur im Zusammenhang mit der Division mit Rest verstehe. Es ist mir noch nicht ganz klar. Danke auf jeden Fall.

---

Ja, dann berechne doch immer jeweils den Rest. Nicht komplizierter denken als nötig.

\( 4+3 = 7 \equiv 2 \mod 5 \)

\( 2 \cdot 7 = 14  \equiv 4 \mod 5 \)

Answer 2

Du kannst auch einfach die Determinante modulo 5 berechnen. Das bietet sich hier an, weil in der 3. Koordinate nur ein Vektor einen von null verschiedenen Eintrag hat. Entwicklung nach der 3. Zeile gibt:

$$\det (v_1\: v_2\: v_3) \equiv_5 -4(3\cdot 4 -2\cdot 1) \equiv_5 -4\cdot 10 \equiv_5 0$$

Die Vektoren sind also in \(\mathbb F_5\) linear abhängig.

Comments

Unser Professor hat die Determinante noch nicht behandelt. Ich habe es aber bereits geschafft, die Lösung zu finden, ohne die Determinante zu verwenden.