Aufstellen von Funktionsgleichungen 3.Grades

Question

Benötige  Hilfe, muss morgen beide Aufgaben erklären können, sitze schon 4 h und bin am verzweifeln...BITTE helft mir so schnell wie mögich...! Danke euch.

Aufgabe 1 )
a) Bestimmen Sie eine ganz rationale Funktion f dritten Grades, deren Graph im Punkt A(-2/-6) einen Extrempunkt und im Punkt B(0/2) einen Wendepunkt besitzt.

b) Existieren neben dem Punkten A) und B) noch weitere Extrem- und Wendepunkte?

Aufgabe 2)

a) Bestimmen Sie eine ganz rationale Funktion g dritten Grades mit folgenden Eigenschaften:
1) Der Graph Gg besitzt im Punkt A(-2/-1) einen Terassenpunkt

2) Die Tangente an dem Graphen Gg im Punkt (-1/?) ist parallel zur Geraden h mit der Gleichung 13,5x+2y+5=0

Zeichnen Sie den Graphen

Answer 1

 

Aufgabe 1)

Ganzrationale Funktion 3. Grades lautet allgemein f(x) = ax³ + bx² + cx + d

Der Punkt A(-2/-6) liegt auf dem Graphen der Funktion, also

f(-2) = -8a + 4b - 2c + d = -6

Er hat dort einen Extrempunkt, das heißt, f'(x) ist dort = 0

f'(x) = 3ax² + 2bx + c

f'(-2) = 12a - 4b + c = 0

B(0|2) liegt auf dem Graphen, also

f(0) = a*0³ + b*0² + c*0 + d = 2

Die Funktion hat in B einen Wendepunkt, also f''(x) = 0

f''(x) = 6ax + 2b

f''(0) = 6a*0 + 2b = 0

a = -0,5

b = 0

c = 6

d = 2

Die gesuchte Funktion lautet also

f(x) = -0,5x³ + 6x + 2

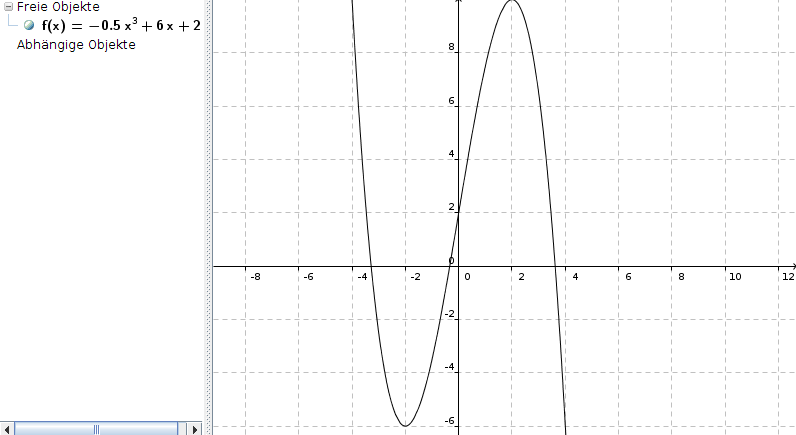
b) Existieren neben dem Punkten A) und B) noch weitere Extrem- und Wendepunkte?

Extrempunkte? f'(x) = 0

f'(x) = -1,5x² + 6 = 0

1,5x² = 6 | : 1,5

x² = 4

x_1,2 = ± √4

Hinreichende Bedingung für Extremum:

f''(x) ≠ 0

f''(x) = - 3x

f''(2) = -6 < 0

Also Maximum in (2|f(2)) = (2|10)

 

Wendepunkte?

f''(x) = -3x = 0

x = 0

B ist der einzige Wendepunkt.

 

Besten Gruß

Comments

Schön, soweit war es mir auch klar, nur ich komm mit dem Additionsverfahren nicht klar..ich komme zwar auf die d und b , aber a und c) fehlt ich kanns nicht löse :-(((((((

---

I. -8a + 4b - 2c + d = -6

II. 12a - 4b + c = 0

III. a*0³ + b*0² + c*0 + d = 2

IV. 6a*0 + 2b = 0

 

Aus III. folgt d = 2, aus IV. folgt b = 0

Das können wir in I. und II. einsetzen:

I. -8a - 2c = -8

II. 12a + c = 0

I. + 2 * II ergibt

16a = -8

a = -0,5

Das eingesetzt in II.

-6 + c = 0

c = 6

 

Wenn Du einen vernünftigen Taschenrechner benutzen darfst, löst er Dir das im Nu unter

"Simultaneous Linear Equations" oder ähnlich :-)

---

muss beim einsetzten in den extrempunkt -2 mal 3 und dann hoch 2 gerechnet werden? weil wenn ja ist das ergebnis nicht 36 und nicht 12?

---

hat sich erledigt xDDDD

Answer 2

Hi,

Aufgabe 1)

a)

Stelle die Bedingungena uf:

f(-2) = -6

f'(-2) = 0

f(0)=2

f''(0)=0

 

Es ergibt sich folgendes Gleichungssystem:

-8a + 4b - 2c + d = -6

12a - 4b + c = 0

d = 2

2b = 0

 

Löse dies:

f(x) = -0,5x^3 + 6x + 2

 

b)

Da Du eine Funktion 3ten Grades hast. Und schon einen Wendepunkt und ein Extrema hast, muss es auch ein zweites Extrema geben. Das liegt gleich weit auf der anderen Seite des Wendepunktes (Punktsymmetrie zum Wendepunkt). Das ist also für x = 2 der Fall.

Dann noch die y-Werte bestimmen:

T(-2|-6) und H(2|10)

Der Wendepunkt war W(0|2).

 

Grüße

Comments

Aufgabe 2)

a) Bestimmen Sie eine ganz rationale Funktion g dritten Grades mit folgenden Eigenschaften:
1) Der Graph Gg besitzt im Punkt A(-2/-1) einen Terassenpunkt

2) Die Tangente an dem Graphen Gg im Punkt (-1/?) ist parallel zur Geraden h mit der Gleichung 13,5x+2y+5=0

Zeichnen Sie den Graphen

 

Aus 1)

f(-2) = -1

f'(-2) = 0

f''(-2) = 0

Aus 2)

f'(-1) = -6,75    (Die Steigung von h ist m = -6,75, damit auch die Steigung der Tangente)

 

Es ergibt sich das Gleichungssystem:

-8a + 4b - 2c + d = -1

12a - 4b + c = 0

-12a + 2b = 0

3a - 2b + c = -6,75

 

Löse das Gleichungssystem:

f(x) = -2,25x^3 - 13,5x^2 - 27x - 19

 

Alles klar?

---

Aber wie löse ich das Gleichungssystem mit den Addition verfahren? Hilfe bitte ausführlich danke

Answer 3

1)

3.Grad   Der Graph Gg besitzt im Punkt A\((-2|-1)\) einen Terrassenpunkt.

Ich verschiebe den Graph um 1 Einheit nach oben

A\((-2|-1)\)→ A´\((-2|0)\)  Nun ist hier eine Dreifachnullstelle:

\(f(x)=a(x+2)^3\)

2) Die Tangente an dem Graphen Gg im Punkt (-1/?) ist parallel zur Geraden h mit der Gleichung 13,5x+2y+5=0

\(13,5x+2y+5=0\)  Steigung der Geraden \(m=-6,75\)

\(f´(x)=3a(x+2)^2\)

\(f´(-1)=3a(-1+2)^2=3a\)

\(3a=-6,75\)

\(a=-2,25\)

\(f(x)=-2,25(x+2)^3\)

Um eine Einheit nach unten:

\(p(x)=-2,25(x+2)^3-1\)