Aufgabe: Stochastische Matrizen
Kann mir jemand erklären was ich an meinen Ansatz falsch gemacht habe?
Text erkannt:
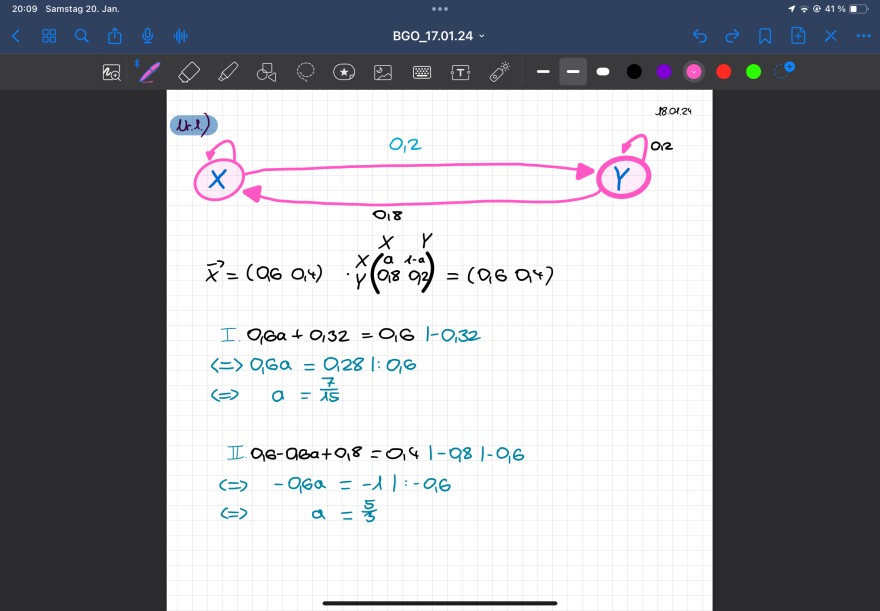
1 Für einen Austauschprozess gilt der Stabilitätsvektor \( \vec{x}=(0,6 \quad 0,4) \) und das nebenstehende Diagramm.
Bestimmen Sie die Übergangsmatrix A.
Übertragen Sie das Diagramm in Ihr Heft und vervollständigen Sie es.
Text erkannt:
20:09 Samstag 20. Jan.
ar. l.)
18.0124
\( \vec{x}=\left(\begin{array}{lll} 0,6 & 0,4 \end{array}\right) \quad \cdot \begin{array}{cc} x & y \\ x & \left(\begin{array}{ll} a & 1-a \\ 0,8 & 02 \end{array}\right) \end{array}=\left(\begin{array}{ll} 0,6 & 0,4 \end{array}\right) \)
\( \begin{array}{l} \text { I } 0,6 a+0,32=0,61-0,32 \\ \Leftrightarrow 0,6 a=0,281: 0,6 \\ \Leftrightarrow a=\frac{7}{15} \end{array} \)
II \( 0,6-0,3 a+0,8=0,4|-0,8|-0,6 \)
\( \begin{aligned} & \Leftrightarrow & -0,6 a & =-1 \mid:-0,6 \\ & \Rightarrow & a & =\frac{5}{3} \end{aligned} \)